Проекция инвариантной меры с орбиты коприсоединенного представления на подалгебру Картана

С.В. Никитин, Омский государственный университет, кафедра математического анализа

1. Введение

В 1973 г. Костант в своей работе [1] показал, что если G компактная группа и ее алгебра Ли, то для элемента X из подалгебры Картана алгебры выполнено равенство

где - ортогональная проекция (относительно формы Киллинга); - группа Вейля алгебры , означает выпуклую оболочку множества A.

Теорема Костанта о выпуклости является обобщением более ранних результатов Шура и Хорна. В 1923 г. Шур доказал, что диагональ эрмитовой матрицы A=(aij) порядка n с собственными числами содержится в выпуклой оболочке множества , где Sn - симметрическая группа, действующая на перестановками координат. Затем Хорн показал, что каждая точка этой выпуклой оболочки может быть получена таким способом.

Таким образом, проекция орбиты - это выпуклый многогранник с вершинами в точках . В 1982 г. Guillemin и Stenberg [2], а также Atiyah [3] дали интерпретацию теоремы Костанта как теоремы о выпуклости отображения моментов. Следующий естественный шаг - нахождение проекции инвариантной меры с орбиты на подалгебру Картана. Существует формула Duistermaat-Heckman'а [4, 5] для преобразования Лапласа проекции инвариантной меры, по которой она может быть восстановлена, но представляет интерес и прямая геометрическая конструкция для нахождения проекции инвариантной меры, которая предложена в этой статье.

2. Предварительные сведения

Пусть - конечномерная вещественная простая компактная алгебра Ли, - ее подалгебра Картана. Группа Ли G алгебры действует на с помощью коприсоединенного представления : , где , . Определим орбиту элемента :

На каждой орбите существует единственная с точностью до пропорциональности инвариантная мера , т.е. такая, что для любой непрерывной функции и для любого

Пусть ортогональная проекция. Определим проекцию меры на - это мера , задаваемая соотношением:

где - финитная непрерывная функция на . Мера абсолютно непрерывна и , где - плотность проекции меры . Нахождению плотности и посвящена эта статья.

Введем некоторые обозначения: - система корней алгебры , - множество положительных корней, - их полусумма. Пусть - решетка весов алгебры , кроме того, пусть обозначает множество , где - камера Вейля. представляет собой множество всех старших весов . Каждому неприводимому представлению группы G соответствует единственный старший вес . Если - характер этого представления, то формула Кириллова утверждает, что

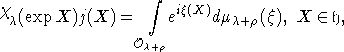
где

Интеграл в правой части формулы Кириллова можно понимать как обратное преобразование Фурье от функции :

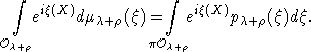
Таким образом, формулу Кириллова можно переписать в следующем виде:

или

Пусть неприводимое представление . Обозначим множество весов как . Если , то обозначает кратность веса в представлении . Известно, что

Рекомендуем скачать другие рефераты по теме: реферат на тему образование, виды понятий реферат.



1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки