Предыдущая страница реферата | 1  2  3

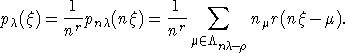
Для вычисления используется формула Костанта для кратностей весов. Если , то

Затем обе части равенства умножаются на непрерывную финитную функцию , интегрируются по и, наконец, n устремляется к бесконечности (при этом сумма в правой части рассматривается как интегральная сумма). После некоторых преобразований получается следующее равенство:

Так как это верно для любой непрерывной функции , то получаем (*) для всех После этого, используя однородность функции , (*), доказывается для всех , , где , , а затем, используя предельный переход, и для всех . Непрерывность и кусочно-полиномиальность следуют из соответствующих свойств функции .

Докажем инвариантность относительно действия группы Вейля, т.е. равенство . Так как для функции j(X) выполнено равенство j(wX)=j(X), то верно и . Далее, если , то

Затем равенство доказывается для всех . Из равенства (*) легко получить, что . Так как функция -инвариантна, то .

Список литературы

Kostant B. On convexity, the Weyl group and the Iwasawa decomposition // Ann. Sci. Ecole Norm. Sup. 1973. N.6. С.413-455.

Guillemin V., Stenberg S. Convexity properties of the moment mapping // Invent. Math. 1982. N.67. С.491-513.

Atiyah M. Convexity and commuting hamiltonians // Bull. London Math. Soc. 1982. N.14. С.1-15.

Duistermaat J. J., and Heckman G. J. On the variation in the cohomology in the symplectic form of the reduced phase space // Invent. Math. 1982. N.69. С.259-268.

Neeb K.-H. A Duistermaat-Heckman formula for admissible coadjoint orbits, preprint.

Скачали данный реферат: Изюмов, Жеффре, Kologreev, Kachusov, Купцов, Sigov.
Последние просмотренные рефераты на тему: сообщение, реферат на тему дети, сочинение ревизор, 6 решебник виленкин.



Предыдущая страница реферата | 1  2  3

Поделитесь этой записью или добавьте в закладки