Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Для нерелятивистских частиц τ3= 44/(EL).

Рассмотренным периодическим движениям соответствуют некоторые величины, сохраняющиеся (в среднем) при движении частицы, если за время, характерное для данного типа движения: (τ1,τ2,τ3), изменением магнитного поля можно пренебречь:

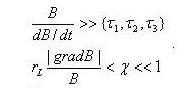(3.2.9)

Эти величины называются адиабатическими инвариантами движения частиц.

Первым адиабатическим инвариантом является магнитный момент частицы

Второй, или продольный инвариант (инвариант продольного действия)

(3.2.10)

Используя эти два инварианта, а также то, что Е = const в постоянном магнитном поле, можно показать, что в дипольном поле частицы с разными энергиями и питч-углами, находящиеся на одной силовой линии, при дрейфе вокруг Земли движутся практически по одной и той же оболочке (дрейфовой оболочке). Поэтому трехмерное представление захваченной радиации сводится к двумерному и характеризуется функцией двух координат: L = Rэ/Rз и В.

В том случае, когда точки отражения захваченных частиц находятся на малых высотах над поверхностью Земли, для учета влияния атмосферы на захваченные частицы вводят параметр hmin, представляющий минимальную высоту над поверхностью Земли, на которую опускается частица на данной дрейфовой оболочке L.

Третий инвариант Ф определяется как поток геомагнитного поля через экваториальную плоскость вне данной L-оболочки. При B/(dB/dt)~τ3 третий инвариант сохраняться не будет, но поскольку при этом В/(dB/dt) > (τ1 ,τ2), первые два инварианта μ и I сохраняются. Магнитное поле на данной L-оболочке будет меняться, при этом E/B=const вследствие сохранения μ, и частица может перейти на другую L-оболочку с соответствующим изменением Е.

Если B/(dB/dt)~{τ1, τ2}, то ларморовское движение частицы и ее колебания между точками отражения нельзя считать независимыми движениями. При этом нарушается μ и J, экваториальный питч-угол частицы изменяется, и она может высыпаться в атмосферу. При большом импульсе частицы

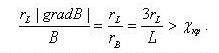(3.2.11)

Здесь rB – радиус кривизны магнитной силовой линии на экваторе. В дипольном поле rB=L/3. В таком случае частица не может находиться в магнитной ловушке в захваченном состоянии и быстро покидает ее. Согласно экспериментальным данным (Ильин, Кузнецов, 1975) χкр~0.1, это соответствует

(3.2.12)

Для протонов это приводит к следующему выражению для максимальной энергии частиц, захваченных на данной L-оболочке (нерелятивистский случай):

(3.2.13)

По расчетам (Кузнецов, Юшков, 2002) χкр=0.109exp(1.928sin2α).

1.2 Движение частицы при наличии электрического поля

Для объяснения многих явлений в магнитосфере Земли необходимо допустить существование электрического поля ε, перпендикулярного магнитному. При этом на движение ведущего центра частицы вокруг Земли накладывается дрейф в направлении, перпендикулярном электрическому и магнитному полю со скоростью Vε (смс-1): Vе = 157ε/B , 3.2.14 где ε - напряженность электрического поля в кВ/Rз, B – магнитное поле в Гс. Траекторию движения ведущего центра в плоскости экватора (αэ = 90°) можно вычислить, исходя из законов сохранения энергии и магнитного момента : Е + U = const , μ = const , 3.2.I5 где U - электрический потенциал данной точки пространства. Вид траекторий дрейфа электронов в однородном электрическом поле показан на рис. 3.2.la.

Подобный вид имеют и траектории электронов ионосферного происхождения, лишь разность между Lкр и Lmin больше, чем для высокоэнергичных электронов. Область замкнутых траекторий для ионосферных электронов качественно соответствует области плазмосферы. Для протонов больших энергий траектории подобны траекториям энергичных электронов, но зеркальны относительно линии, проходящей через центр Земли в направлении на Солнце.

Видно, что траектории, проходящие на больших расстояниях от Земли, разомкнуты. Частицы, находящиеся на замкнутых орбитах, принадлежат радиационным поясам.

Точку ветвления Lкр на критической орбите можно найти, приравняв скорости электрического и магнитного дрейфов частиц вокруг Земли:

.

Для нерелятивистских частиц получаем:

(3.2.I6)

здесь и далее Е в кэВ. Из этой формулы можно определить, частицы каких энергий на данном L принадлежат радиационным поясам. С противоположной стороны частицы проходят на минимальном расстоянии от Земли:

Рекомендуем скачать другие рефераты по теме: диплом государственного образца, реферат образование.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки