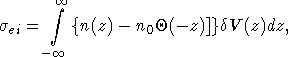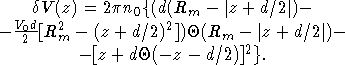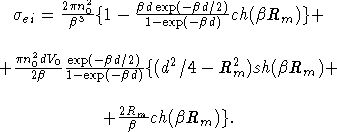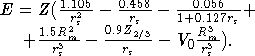где
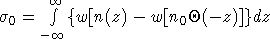 - вклад от
электронной системы в рамках модели "желе", когда заряд положительных
ионов в металле считается равномерно и непрерывно размазанным по всему объему;
- вклад от
электронной системы в рамках модели "желе", когда заряд положительных
ионов в металле считается равномерно и непрерывно размазанным по всему объему; 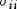 возникает от
электростатического взаимодействия ионов между собой;
возникает от
электростатического взаимодействия ионов между собой; 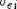 - связан с разностью в электростатическом
взаимодействии электронов с дискретными ионами и с однородным фоном
"желе". Для
- связан с разностью в электростатическом
взаимодействии электронов с дискретными ионами и с однородным фоном
"желе". Для 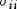 можно
воспользоваться аналитическим выражением работы [5]:
можно
воспользоваться аналитическим выражением работы [5]:
|
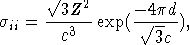
|
(6)
|
где
Z - валентность ионов; с - расстояние между ближайшими соседями в плоскости
параллельной поверхности; d - межплоскостное расстояние.
Для
вычисления поправки на электрон-ионное взаимодействие воспользуемся широко
применяемым в физике металлов обобщенным псевдопотенциалом Хейне-Абаренкова.
Явный вид данного псевдопотенциала можно записать следующим образом:
|
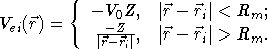
|
(7)
|
Псевдопотенциал
Хейне-Абаренкова переходит в выражение для другого широко используемого
псевдопотенциала Ашкрофта при V0=0. Для получения 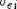 нами была
использована методика, развитая в работе [6], согласно которой
нами была
использована методика, развитая в работе [6], согласно которой
|
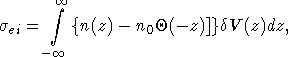
|
(8)
|
где
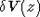 имеет смысл среднего
по плоскостям от суммы ионных псевдопотенциалов за вычетом потенциала
полубесконечного однородного фона заряда. Нами было получено для
имеет смысл среднего
по плоскостям от суммы ионных псевдопотенциалов за вычетом потенциала
полубесконечного однородного фона заряда. Нами было получено для 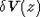 при
-d<z<0 следующее выражение:
при
-d<z<0 следующее выражение:
|
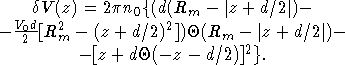
|
(9)
|
Проводя
суммирование по ионным плоскостям с z=-(i+d/2), i=1,2,... и воспользовавшись
периодичностью потенциала 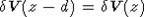 , из (8)
получим
, из (8)
получим
|
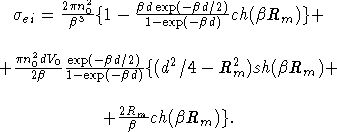
|
(10)
|
Проводя
численное интегрирование и минимизацию полной поверхностной энергии (5), определяем параметр 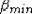 , а затем и
само значение
, а затем и
само значение 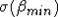 . В настоящей
работе для определения параметров псевдопотенциала Хейне-Абаренкова
использовалось условие минимума объемной энергии металла при наблюдаемом
равновесном атомном объеме
. В настоящей
работе для определения параметров псевдопотенциала Хейне-Абаренкова
использовалось условие минимума объемной энергии металла при наблюдаемом
равновесном атомном объеме 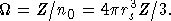 В соответствии
с приближением локальной плотности объемная энергия металла выражалась через
параметр плотности rs :
В соответствии
с приближением локальной плотности объемная энергия металла выражалась через
параметр плотности rs :