Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Пример 4. Решим уравнение .

Возведя в квадрат обе части этого уравнения, получаем , , . Подстановкой убеждаемся, что число 5 не является корнем данного уравнения. Поэтому уравнение не имеет решений.

Пример 5. Решим уравнение .

По определению  - это такое неотрицательное число, квадрат которого равен подкоренному выражению. Другими словами, уравнение равносильно системе:

  

 

Решая первое уравнение системы, равносильное уравнению , получим корни 11 и 6, но условие  выполняется только для . Поэтому данное уравнение имеет один корень .

Пример 6. Решим уравнение .

В отличие от рассмотренных ранее примеров данное иррациональное уравнение содержит не квадратный корень, а корень третьей степени. Поэтому для того, чтобы “избавиться от радикала”, надо возвести обе части уравнения не в квадрат, а в куб: . После преобразований получаем:

Итак, , .

Пример 7. Решим систему уравнений:

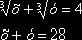
Положив  и , приходим к системе

Разложим левую часть второго уравнения на множители:  - и подставим в него из первого уравнения . Тогда получим систему, равносильную второй:

Подставляя во второе уравнение значение v, найденное из первого , приходим к уравнению , т.е. .

Полученное квадратное уравнение имеет два корня:  и .

Соответствующие значения v таковы:  и . Переходя к переменным х и у, получаем: , т.е. , , , .

Преобразование иррациональных выражений.

Если знаменатель дроби содержит иррациональное выражение, то часто целесообразно избавиться от последнего.

Рассмотрим некоторые типичные случаи:

 

Пример:

Рекомендуем скачать другие рефераты по теме: реферат на тему рынок, курсовые.



Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки