Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

   Методы Рунге-Кутта обладают следующими свойствами:

1. Эти методы являются одноступенчатыми: чтобы найти уm+1, нужна информация  о предыдущей точке xm,ym.

2. Они согласуются с рядом Тейлора вплоть до членов порядка hp, где степень р различна для различных методов и называется порядковым номером или порядком метода.

3. Они не требуют вычисления производных от f (x,y), а требуют вычисления самой  функции.

Рассмотрим сначала геометрическое построение и выведем некоторые формулы на основе геометрических аналогий. После этого мы подтвердим полученные результаты аналитически.

   Предположим, нам известна точка xm,ym  на  искомой кривой. Тогда мы можем провести прямую линию с тангенсом угла наклона у¢m=f(xm,ym), которая пройдет через точку xm,ym. Это построение показано на рис.1, где кривая представляет собой точное, но конечно неизвестное решение уравнения, а прямая линия L1 построена так, как это только что описано.

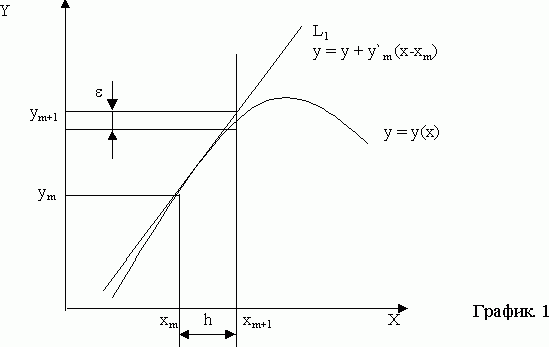
Тогда следующей точкой решения можно считать ту, где прямая L1 пересечет ординату, проведенную через точку x=xm+1=xm+h.

Уравнение прямой L1 выглядит так: y=ym+y¢m(x-xm) так как y¢=f(xm,ym) и кроме того, xm+1=xm+h тогда уравнение примет вид 

ym+1=ym+h*f(xm,ym)                                                                                1.1

   Ошибка при x=xm+1 показана в виде отрезка е. Очевидно, найденное таким образом приближенное значение согласуется с разложением в ряд Тейлора вплоть до членов порядка h, так что ошибка ограничения равна  et=Кh2

   Заметим, что хотя точка на графике 1 была показана на кривой, в действительности ym является приближенным значением и не лежит точно на кривой.

   Формула 1.1 описывает метод Эйлера, один из самых старых и широко известных методов численного интегрирования дифференциальных уравнений. Отметим, что метод Эйлера является одним из методов Рунге-Кутта первого порядка.

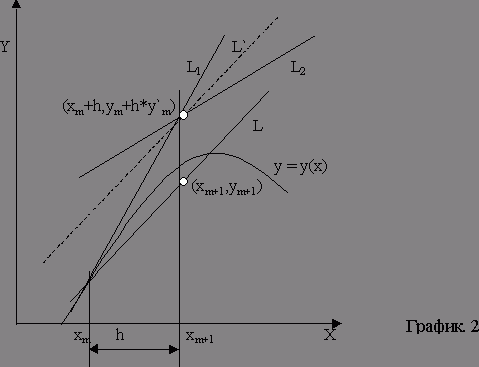
Рассмотрим исправленный метод Эйлера и модификационный метод Эйлера. В исправленном методе Эйлера мы находим средний тангенс угла наклона касательной для двух точек: xm,ym и xm+h,ym+hy¢m. Последняя точка есть та самая, которая в методе Эйлера обозначалась xm+1,ym+1. Геометрический процесс нахождения точки xm+1,ym+1 можно проследить по рис.2. С помощью метода Эйлера находится точка xm+h,ym+hy¢m, лежащая на прямой L1. В этой точке снова вычисляется тангенс, дает прямую L. Наконец, через точку xm,ym мы проводим прямую L, параллельную L. Точка, в которой прямая L пересечется с ординатой, восстановленной из x=xm+1=xm+h, и будет искомой точкой xm+1,ym+1.

Тангенс угла наклона прямой L и прямой L равен

Ф(xm,ym,h)=½[f(xm,ym)+f(xm+h,ym+y¢mh)]                                                           1.2

  

где  y¢m=f(xm,ym)                                                                                                1.3

   Уравнение линии L при этом записывается в виде

               y=ym+(x-xm)Ф(xm,ym,h),

   так что

                           ym+1=ym+hФ(xm,ym,h).                                                              1.4

   Соотношения 1.2, 1.3, 1.4 описывают исправленный метод Эйлера.

Чтобы выяснить, насколько хорошо этот метод согласуется с разложением в ряд Тейлора, вспомним, что разложение в ряд функции f(x,y) можно записать следующим образом:

   f(x,y)=f(xm,ym)+(x-xm)¶f/¶x+(y-ym)¶f/¶x+¼                                         1.5

где частные производные вычисляются при x=xm и y=ym.

Рекомендуем скачать другие рефераты по теме: доклад 2011, шпори для студентів.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки