Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

   Подставляя в формулу 1.5 x=xm+h и y=ym+hy¢m и используя выражение 1.3 для y¢m, получаем

               f(xm+h,ym+hy¢m)=f+hfx+hffy+O(h2),

где снова функция f и ее производные вычисляются в точке xm,ym. Подставляя результат в 1.2 и производя необходимые преобразования, получаем

               Ф(xm,ym,h)=f+h/2(fx+ffy)+O(h2).

Подставим полученное выражение в 1.4 и сравним с рядом Тейлора

               ym+1=ym+hf+h2/2(fx+ffy)+O(h3).

   Как видим, исправленный метод Эйлера согласуется с разложением в ряд Тейлора вплоть до членов степени h2, являясь, таким образом, методом Рунге-Кутты второго порядка.

Рассмотрим модификационный метод Эйлера. Рассмотрим рис.3 где первоначальное построение сделано так же, как и на рис.2. Но на этот раз мы берем точку, лежащую на пересечении этой прямой и ординатой x=x+h/2. На рисунке эта точка образована через Р, а ее ордината равна y=ym+(h/2)y¢m. Вычислим тангенс угла наклона касательной в этой точке

               Ф(xm,ym,h)=f+(xm+h/2,ym+h/2*y¢m),                                                     1.6

   где       y¢m=f(xm,ym)                                                                                                     1.7

   Прямая с таким наклоном, проходящая через Р, обозначена через L*. Вслед за тем, мы проводим через точку xm,ym прямую параллельную L*, и обозначаем ее через L0. Пересечение этой прямой с ординатой x=xm+h и даст искомую точку xm+1,ym+1. Уравнение прямой можно записать в виде y=ym+(x-xm)Ф(xm,ym,h),

где Ф задается формулой 1.6. Поэтому

ym+1=ym+hФ(xm,ym,h)                                                                                         1.8

Соотношения 1.6, 1.7, 1.8 описывают так называемый модификационный метод Эйлера и является еще одним методом Рунге-Кутта второго порядка. Обобщим оба метода. Заметим, что оба метода описываются формулами вида

           ym+1=ym+hФ(xm,ym,h)                                                                              1.9

и в обоих случаях Ф имеет вид

Ф(xm,ym,h)=a1f(xm,ym)+a2f(xm+b1h,ym+b2hy¢m),                                                 1.10

где       y¢m=f(xm,ym)                                                                                                           1.11

   В частности, для исправленного метода Эйлера

               a1=a2=1/2;

               b1=b2=1.

В то время как для модификационного метода Эйлера

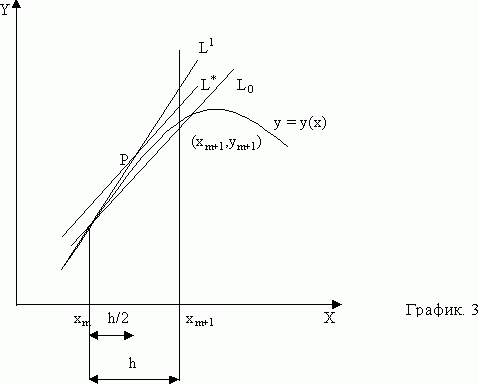               a1=0, a2=1,      

               b1=b2=1/2.

Формулы 1.9, 1.10, 1.11 описывают некоторый метод типа Рунге-Кутты. Посмотрим, какого порядка метод можно рассчитывать получить в лучшем случае и каковы допустимые значения параметров a1, a2, b1 и b2 .

   Чтобы получить соответствие ряду Тейлора вплоть до членов степени h, в общем случае достаточно одного параметра. Чтобы получить согласование вплоть до членов степени h2, потребуется еще два параметра, так как необходимо учитывать члены h2fx и  h2ffy. Так как у нас имеется всего четыре параметра, три из которых потребуются для создания согласования с рядом Тейлора вплоть до членов порядка h2, то самое лучшее, на что здесь можно рассчитывать - это метод второго порядка.

Рекомендуем скачать другие рефераты по теме: доклад 2011, шпори для студентів.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки