Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

На основе последовательного применения к термодинамическим системам (системам состоящим из несчётного числа частиц) закона сохранения результирующего импульса покажем единство динамики малого числа частиц (динамики Ньютона) и динамики несчётного числа частиц (термодинамики). Рассмотрим процессы возникновения кооперативных векторных потоков энергии в неравновесных многочастичных системах и условия, при которых происходит или их затухание, вплоть до равновесного состояния, или формирование диссипативных структур Пригожина.

В учении о тепле факт равновесного состояния и неизбежности его наступления для замкнутой многомолекулярной системы имеет особое, основополагающее значение. Все фундаментальные выводы термодинамики и статистической физики построены на этом факте.

Рассмотрим это наиболее общее свойство всех многомолекулярных систем, т.е. их стремление к равновесию, постараемся раскрыть механизм релаксации подобных систем. Известно, что это свойство обусловлено столкновением частиц между собой и со стенками сосуда. Так вот, возникает вопрос, а как в процессе столкновения частиц между собой и со стенками сосуда направленное движение приходит в равновесное состояние, т.е. каким образом кинетическая энергия направленного движения (кооперативная энергия общего движения частиц) переходит в кинетическую энергию хаотически движущихся частиц?

На первый взгляд покажется вполне понятным и естественным, что если одна или несколько направленно движущихся частиц высокой энергии сталкиваются с большой массой хаотически движущихся частиц, то в результате сталкивания направленные частицы перемешиваются и их направленная энергия будет рассеяна. Однако при таком подходе происходит подмена сложного на хаотическое. При ближайшем рассмотрении выясняется четкий, имеющий свои границы, механизм релаксации, механизм установления равновесия, вытекающий из законов механики.

Во первых покажем что результирующий импульс всех частиц системы, находящейся в равновесии, равен нулю как вектор.

где n-количество частиц в системе.

Обоснование данного утверждения легко провести с помощью выводов статистической физики. Известно, что в случае равновесного состояния в газе всегда реализуется Максвеловское распределение по скоростям. В статистической физике показывается, что для случая Максвеловского распределения по скоростям средняя проекция скорости хаотического движения на любое направление оказывается равной нулю. А если равна нулю проекция средней скорости, то равна нулю и проекция среднего импульса на любое направление. И результирующий импульс равен нулю как вектор.

Теперь рассмотрим замкнутую систему из 10-и частиц, находящихся в покое (для простоты будем рассматривать механическую модель газа - абсолютно упругие шары). Этой замкнутой системе извне передадим импульс . Наиболее характерным свойством этой замкнутой системы, с точки зрения динамики, будет, наряду с сохранением полной энергии то, что этот импульс будет сохраняться постоянным по величине и направлению, сколько бы частицы не сталкивались между собой. При рассмотрении замкнутой системы из 20, 100 частиц свойство сохраняется. Теперь же рассмотрим замкнутую систему из многих и многих миллиардов частиц. Здесь положение коренным образом меняется. Наиболее характерным свойством этой системы является стремление к равновесию, при котором как было показано выше результирующий импульс всех молекул равен нулю как вектор, т.е. направленное движение перейдет в хаотическое. Таким образом с одной стороны для замкнутой механической системы имеем с другой, при увеличении числа частиц системы, имеем прямо противоположное свойство , направленное движение исчезает. Попытаемся выяснить, каким образом разрешается этот парадокс, т.е. рассмотрим механизм релаксации. Каким образом кооперативная кинетическая энергия направленного движения с переходит в кинетическую энергию хаотически движущихся частиц с как вектор? Взаимодействие молекул (шаров) будем описывать законами абсолютно-упругого удара. Так как молекулы имеют конечные размеры, то удар будет нецентральный. Обратим на это особое внимание. Это ключ к решению поставленной задачи. Вероятность центрального удара, согласно положениям статистической физики в системе свободных частиц стремится к нулю. Если не нравятся абсолютно-упругие шары будем понимать под ними силовые поля, имеющие форму шара или круговые эффективные сечения взаимодействия. Причём шаровые силовые поля рассматриваем для упрощения модели, что бы заострить внимание на главном виновнике рассеяния кооперативной энергии – нецентральном соударении.

Пусть имеем замкнутую систему, состоящую из одинаковых шаров. Причем n шаров покоятся, а один шар движется и сталкивается с покоящимися шарами. До столкновения результирующий импульс системы: , т.е. равен импульсу движущегося шара, а кинетическая энергия равна кинетической энергии движущегося шара. Причем кинетическая энергия строго направлена по результирующему импульсу системы, вся переносима этим результирующим импульсом.

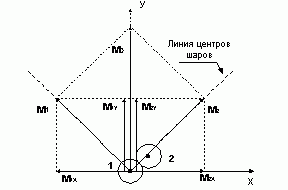
Шар 1 (см. рис.1) сталкивается с покоящимися шарами, причем должны при этом выполняться закон сохранения результирующего импульса и закон сохранения кинетической энергии. Пишу закон сохранения кинетической, а не полной энергии, т.к. принято считать что при абсолютно-упругом соударении шаров потенциальная энергия проявляется только в момент непосредственного соприкосновения. Эта схема принимается мною с тем что бы в наибольшей простоте раскрыть механизм рассеяния кооперативной кинетической энергии. При рассмотрении последовательности столкновений будем следить не за траекториями отдельных частиц, которые экспоненциально разбегаются, а за поведением результирующего импульса.

Шар 1 с импульсом после столкновения с первым шаром 2 будет иметь импульс , а шар 2 приобретет импульс которые в сумме (геометрической) дадут первоначальный импульс . Закон сохранения импульса соблюден. Разложим импульсы шаров 1 и 2 после столкновения на оси и . Проекции и дадут в сумме первоначальный импульс , а проекции , перпендикулярные первоначальному результирующему импульсу на его величину после столкновения не влияют и в сумме дают нуль-вектор. Равенство по абсолютной величине импульсов и легко видно из векторной диаграммы и вытекает из закона сохранения результирующего импульса. Однако эти два последних уравновешенных импульса (нуль-вектор) несут каждый на себе определенное количество кинетической энергии, полученной от кинетической энергии первоначального импульса .

Так как и

Массы шаров для простоты все равны. Если, как было показано выше, результирующий импульс после столкновения сложится из двух проекций на ось и остался постоянным, то кинетическая энергия, переносимая этим импульсом после столкновения, т.е. проекциями и будет составлять только часть кинетической энергии, переносимой результирующим импульсом до столкновения. Другая часть кинетической энергии, переносимая взаимно уравновешенными импульсами и (нуль-вектором) переходит в хаотическую форму. После следующего соударения теперь уже двух движущихся шаров результирующий импульс сложится из 4-х шаров и произойдет дополнительное рассеяние направленной кинетической энергии и т.д. Таким образом благодаря нецентральному соударению шаров в первоначальный направленный импульс лавинообразно вовлекается все большее и большее число шаров и происходит лавинообразный рост массы результирующего импульса. А по мере вовлечения шаров происходит все большее рассеяние первоначально направленной кинетической энергии. Это видно и из таких простых математических преобразований:

; ;

; m-масса шара ; ; (1)

Так как в результате столкновений в перенос результирующего импульса вовлекается все большее число молекул, то масса результирующего импульса постоянно растет, а скорость результирующего импульса, т.е. общего переноса падает. После рассмотренного соударения масса результирующего импульса возросла вдвое, а скорость уменьшилась вдвое.

 

Но в кинетическую энергию скорость входит в квадрате, поэтому при увеличении массы в два раза и уменьшении в два раза скорости общего переноса кинетическая энергия общего переноса, т.е. та, которую несет результирующий импульс, уменьшилась вдвое.

 

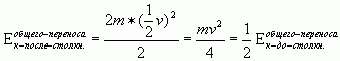
Речь идет о кинетической энергии общего переноса (кооперативной энергии), связанной с результирующим импульсом, т.е. той энергии, которая совершает макроскопическую работу. Закон сохранения общей кинетической энергии системы не нарушается, т.к. адекватно увеличивается хаотическая составляющая кинетической энергии. При увеличении массы, переносящей результирующий импульс, в 10 раз кинетическая энергия, переносимая этим импульсом, и остающаяся в направленной форме, уменьшается в 10 раз. И при стремлении массы результирующего импульса к бесконечности кинетическая энергия общего переноса стремится к нулю. Таким образом при стремлении массы результирующего импульса к бесконечности, т.е. вовлечении в процесс переноса импульса огромного числа частиц, скорость результирующего импульса стремится к нулю и направленное движение затухает. Результирующий импульс, оставаясь постоянным по величине и направлению, вырождается как носитель кооперативной энергии, равносильно тому, что и система приходит в равновесное состояние. Вся кооперативная энергия переходит к нуль-вектору хаоса.

Этим разрешается парадокс который мы выявили в начале. В случае центрального удара рассеяние вообще не происходит. В этом примере мы рассматривали столкновение шара с покоящимися шарами. Картина рассеяния и затухания не изменится, если шары будут не покоиться, а хаотически двигаться с , т.к. причиной рассеяния является не состояние системы, а нецентральное соударение.

Рекомендуем скачать другие рефераты по теме: русский язык 9 класс изложения, сочинение 6 класс.



Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки