Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Визначення: Матриця А зветься невід’ємною, якщо всі її елементи невід’ємні.

Зауваження: Фробеніус довів, що твердження теореми Перрона залишаються в силі для нерозкладних невід’ємних матриць. Це можна довести, просто повторивши наше доведення теореми Перрона для 2х2 матриць у випадку, коли один або обидва діагональних елемента дорівнюють нулю.

Визначення: Квадратна матриця називається стохастичною, якщо

1)

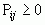
2)

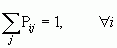
Теорема Маркова: Нехай для стохастичної матриці P існує натуральне число k0 таке, що 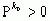(тобто всі елементи додатні). Тоді

1. 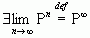(існування границі матриці означає, що існує границя кожного її елементу)

2. Матриця 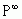- має однакові рядки.

3. Всі елементи цих рядків додатні.

Доведення теореми для 2х2 матриць.

Запишемо стохастичну матрицю у вигляді 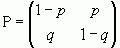, де

Запишемо її характеристичне рівняння: ,

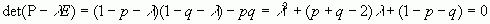
Це квадратне рівняння з дискрімінантом:

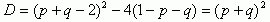
І тому

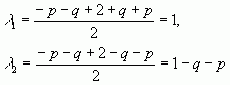
З урахуванням 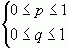маємо 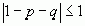, але якщо 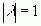, то це значить, що p=q=1 або p=q=0, відкіля матриця P буде мати вигляд 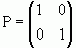, або 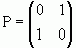і тоді Pn містить нулі 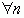, що суперечить умові. Таким чином .

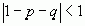Беспосередньою перевіркою з урахуванням стохастичності встановлюємо, що власному значенню 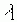відповідає власний вектор 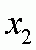, де x1=x2, тобто, наприклад 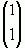власний вектор. Знайдемо власний вектор 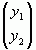, що відповідає власному значенню .

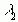За визначенням

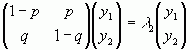
Звідки

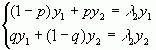
Згадуючи, що 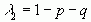отримуємо

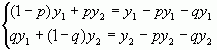
Рекомендуем скачать другие рефераты по теме: профессиональные рефераты, бесплатные доклады.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки