Теория игр и принятие решений
Категория реферата: Рефераты по математике
Теги реферата: шпоры по праву, диплом купить
Добавил(а) на сайт: Кондрат.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
Пример 3. Предположим, что величина спроса x в единицу времени (интенсивность спроса) на некоторый товар задаётся непрерывной функцией распределения f(x). Если запасы в начальный момент невелики, в дальнейшем возможен дефицит товара. В противном случае к концу рассматриваемого периода запасы нереализованного товара могут оказаться очень большими. В обоих случаях возможны потери.
Т.к. определить потери от дефицита очень трудно, ЛПР может установить необходимый уровень запасов таким образом, чтобы величина ожидаемого дефицита не превышала А1 единиц, а величина ожидаемых излишков не превышала А2 единиц. Иными словами, пусть I – искомый уровень запасов. Тогда
ожидаемый
дефицит = 
,
ожидаемые
излишки =
.
При произвольном выборе А1 и А2 указанные условия могут оказаться противоречивыми. В этом случае необходимо ослабить одно из ограничений, чтобы обеспечить допустимость.
Пусть, например,
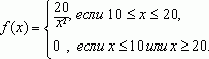
Тогда
= 
= 20(ln 
+
– 1)
= 
= 20(ln 
+
– 1)
Применение критерия предельного уровня приводит к неравенствам
ln I – 
³ ln 20 –
– 1 = 1.996 – 
ln I – 
³ ln 10 –
– 1 = 1.302 – 
Предельные значения А1 и А2 должны быть выбраны так, что бы оба неравенства выполнялись хотя бы для одного значения I.
Например, если А1 = 2 и А2 = 4, неравенства принимают вид
ln I – 
³ 1.896
ln I – 
³ 1.102
Значение I должно находиться между 10 и 20, т.к. именно в этих пределах изменяется спрос. Из таблицы видно, что оба условия выполняются для I, из интервала (13,17)
|
I |
10 |
11 |
12 |
13 |
14 |
15 Рекомендуем скачать другие рефераты по теме: читать рассказы, реферат на тему экология. Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |