Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Ядро гомоморфизма колец является идеалом.

Доказательство.

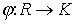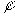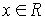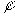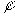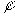Пусть - гомоморфизм колец, I =Ker, - любой элемент. Тогда, (x*I) =(x)* (I) =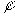(x)*0 =0. Значит, x*I 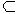Ker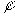 =I. Аналогично проверяется, что I*x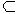I.

Теорема о гомоморфизме для колец.

Пусть 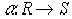- сюръективный гомоморфизм колец. Тогда S изоморфно факторкольцу R/Ker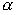. Если эти изоморфные кольца отождествить, то 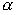отождествляется с естественным гомоморфизмом кольца R на свое факторкольцо.

Доказательство этой теоремы аналогично доказательству соответствующей теоремы для групп и мы его опускаем.

Пример.

Пусть K - кольцо многочленов R[x], 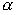: K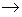C - гомоморфизм, сопоставляющий каждому многочлену p его значение в точке i : 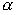(p) =p(i). Ядро этого гомоморфизма составляют многочлены, представимые в виде: (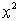+1)*q(x), где q - любой многочлен. Можно записать: Ker 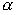=(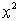+1). По теореме о гомоморфизме .

Кольцо многочленов над полем.

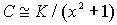Кольцо многочленов над полем (в отличие от случая многочленов над кольцом) обладает рядом специфических свойств, близких к свойствам кольца целых чисел Z .

I. Делимость многочленов.

Хорошо известный для многочленов над полем R способ деления “углом” использует только арифметические действия над коэффициентами и потому применим к многочленам над любым полем k. Он дает возможность для двух ненулевых многочленов p,s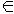k[x] построить такие многочлены q (неполное частное) и r (остаток), что p = q*s +r , причем либо r =0, либо deg(r )< deg(s ). Если r =0 , то говорят, что s делит p (или является делителем p ) и обозначают это так: s | p. Будем называть многочлен унитарным ( или приведенным), если его старший коэффициент равен 1.

Определение.

Общим наибольшим делителем ненулевых многочленов p и s называется такой унитарный многочлен ОНД( p, s), что

ОНД( p, s) | p; ОНД( p, s) | s. q | p, q | s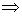 q | ОНД( p, s).

По определению, для ненулевого многочлена р со старшим коэффициентом а ОНД (р, 0) = ОНД (0, р) = р/а; ОНД (0, 0)=0.

Аналогично определяется ОНД любого числа многочленов.

Единственность ОНД двух многочленов непосредственно вытекает из определения. Существование его следует из следующего утверждения.

Основная теорема теории делимости (для многочленов).

Для любых двух ненулевых многочленов p и q над полем k можно найти такие многочлены u и v над тем же полем, что ОНД(p, q)= u*p+v*q.

Доказательство этой теоремы очень похоже на приведенное в лекции доказательство аналогичной теоремы над Z. Все же наметим основные его шаги.

Выберем такие многочлены u и v чтобы сумма w= u*p+v*q имела возможно меньшую степень( но была ненулевой!). Можно при этом считать w унитарным многочленом. Проверим, что w | p. Выполняя деление с остатком, получаем: p= s*w+r. Подставляя это равенство в исходное, находим: r = p - s*w =p - s*(u*p+v*q) = (1-s*u)*p+(-s*v)q = U*p + V*q . Если при этом r 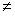0, то deg(r )<deg(w), что противоречит выбору w. Значит, r =0. Аналогично проверяется, что w | q. Обозначим: W = ОНД(p , q). По определению w | W. С другой стороны, W | p, W | q 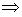W | w. Остается заметить, что оба многочлена w и W унитарные и значит W = w.

Замечание.

Используя индукцию, можно доказать, что для любого числа многочленов ОНД 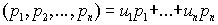для подходящих многочленов 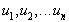. Более того, эта формула сохраняется даже для бесконечного множества многочленов, поскольку их ОНД в действительности является ОНД некоторого их конечного подмножества.

Следствие.

Всякий идеал в кольце многочленов над полем является главным.

В самом деле, пусть p - ОНД всех многочленов, входящих в идеал I. Тогда 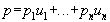, где 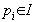. По определению идеала отсюда вытекает, что 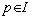, а значит, I =(p).

II. Разложение на множители.

Пусть k некоторое поле, p, q, s - многочлены над k. Если p=q*s, причем оба многочлена q и s имеют степень меньшую, чем p, то многочлен p называется приводимым (над полем k ). В противном случае p неприводим. Неприводимый многочлен в кольце k[x] является аналогом простого числа в кольце Z . Ясно, что каждый ненулевой многочлен p=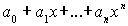 можно разложить в произведение: p= 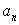*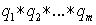, где все многочлены 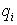неприводимы над k и имеют старший коэффициент равный 1. Можно доказать, что такое разложение единственно с точностью до порядка сомножителей. Разумеется среди этих множителей могут быть одинаковые; такие множители называются кратными. Объединяя кратные множители можно то же разложение записать в виде: p= .

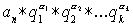Рекомендуем скачать другие рефераты по теме: менеджмент, реферат условия.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки