Предыдущая страница реферата | 1  2  3

Примеры.

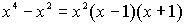. Заметим, что многочлены первой степени по определению неприводимы над любым полем. Множитель x является кратным, остальные - простые. Многочлен 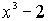неприводим над полем Q рациональных чисел. В самом деле, если (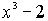)=(x-a)*q, то подставляя в это равенство x=a, получаем: 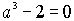, что невозможно ни для какого рационального числа a. Тот же многочлен над полем R вещественных чисел приводим: 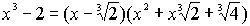, причем второй множитель имеет отрицательный дискриминант и потому далее не разложим над R . Наконец, над полем C комплексных чисел имеем: 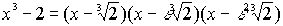, где 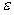=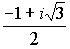- кубический корень из 1. На этом примере мы видим, что понятие приводимости существенно зависит от того над каким полем рассматривается многочлен.

Свойства неприводимых многочленов.

1 .Если p- неприводимый многочлен и d =ОНД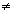(p, q) 1, то p | q.

В самом деле, p = d*s и если deg(s )>0, то это противоречит неприводимости p, а если deg(s )=0, то d | q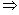p | q.

2. Если p | 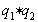и p неприводим, то либо p | 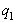либо p | 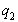. Действительно, в противном случае НОД(p, 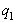) = НОД(p, 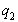) =1 и потому по основной теореме теории делимости 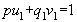; 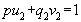, откуда: 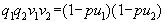и значит, 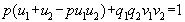, то есть НОД(p, 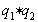)=1 и, следовательно, deg (p )=0.

III. Корни многочленов. Производная и кратные корни.

Пусть p = 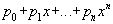некоторый многочлен над k и 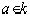. Элемент поля k, равный 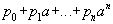, называется значением многочлена p в точке a и обозначается p(a). Соответствие 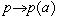является гомоморфизмом 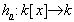Ядро этого гомоморфизма состоит из всех многочленов, для которых p(a) = 0, то есть a является их корнем. Поскольку ядро I - идеал, содержащий (x-a) и не совпадающий с k[x] (x -a +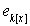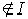), а каждый идеал в k[x] - главный, то I =(x-a). Мы приходим таким образом к теореме Безу : элемент 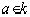будет корнем многочлена p тогда и только тогда, когда (x - a) | p. Отсюда непосредственно вытекает, что неприводимый многочлен степени больше 1 не имеет корней.

Если 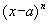| p , то a называется корнем кратности не ниже n. Введем понятие производной многочлена p. По определению это многочлен 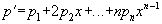. Имеют место обычные правила вычисления производной: 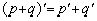; 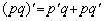. Отсюда следует, что 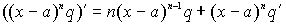и потому наличие у многочлена корня a кратности не ниже n влечет наличие у его производной того же корня кратности не ниже (n-1). В частности, если p(a) = 0, но 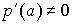, то корень a - простой (то есть не кратный).

Если 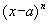| p, но 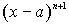не делит p, то число n называется кратностью корня a . Пусть 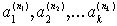- множество всех корней многочлена p с указанными кратностями 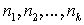. Поскольку при a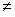b НОД(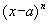,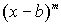) =1, многочлен p делится на 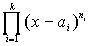и потому deg(p)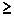 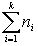. Итак, многочлен степени n имеет не более n корней с учетом их кратности.

Скачали данный реферат: Сильвестров, Gribakin, Tverdislav, Leonila, Manjakin, Ярополов.
Последние просмотренные рефераты на тему: оформление доклада, защита реферата, курсовая работа по менеджменту, оценка дипломной работы.



Предыдущая страница реферата | 1  2  3

Поделитесь этой записью или добавьте в закладки