Теория вероятностей: наука о случайном

Реферат ученика 9 класса «А»  средней школы № 1054 Валишева Тимура

1. Вступление.

С первого взгляда может показаться, что никаких законов, управляющих случайными явлениями нет и быть не может. Однако, если разобраться, случайные явления происходят не так уж хаотически. Во многих случаях обнаруживаются закономерности. Эти закономерности не похожи на обычные законы физических явлений; они весьма разнообразны.

Возьмем, к примеру, игру в монету. При бросании может быть два равновероятных исхода: монета может упасть кверху гербом или решкой. Бросая монету один раз нельзя предугадать, какая сторона окажется сверху. Однако, бросив монету 100 раз, можно сделать выводы. Можно заранее сказать, что герб выпадет не 1 и не 2 раза, а больше, но и не 99 и не 98 раз, а меньше. Число выпадений герба будет близко к 50. На самом деле, и на опыте можно в этом убедиться, что это число будет заключено между 40 и 60.

Так же статистически установлено, что на 1000 детей приходится 511 мальчиков и 489 девочек (т.е. 48,9% и 51,1% соответственно). Это поразительное постоянство отмечено многими учеными, среди которых и Симон Лаплас, один из основателей Теории. Эта информация позволяет нам с большой точностью предсказывать вероятность количества мальчиков или девочек в тот или иной год (эти расчеты, например, используются призывной комиссией).

2. Определения и основные понятия Теории.

Теперь перейдем к алгебраическому выражению Теории. Вот классическое определение:

определение: Пусть множество исходов опыта состоит из n равновероятных исходов. Если m из них благоприятствуют событию A, то вероятностью события A называется число

Давая такое определение, мы рассчитываем, что (в силу равновероятности исходов опыта) при n-кратном повторении опыта событие A наступит в  случаях (именно в этом заключается практическая ценность Теории).

Следует объяснить некоторые понятия Теории, которые будут необходимы в дальнейшем:

Достоверное событие – событие, которое обязательно должно произойти в результате опыта. Такое событие обозначается буквой E (Expected)

Невозможное событие – событие, которое не может произойти в результате опыта. Такое событие обозначается буквой U (Unreal)

Несовместные события – события, которые не могут произойти в результате опыта одновременно.

Совместные события – события, которые могут произойти в результате опыта одновременно.

Событие A благоприятствует событию B, если из того, что произошло событие A следует событие B. (т.е. )

Объединением событий A и B называется событие, состоящее в том, что в результате опыта произошло хотя бы одно из этих событий (т.е. ).

Пересечением событий A и B называется событие, состоящее в том, что в результате опыта произошли оба из этих событий (т.е. ).

Закон больших чисел.

Пусть K раз мы проделали испытания, и N раз в результате опыта произошло событие A. Тогда число  будет называться частотой появления события А. Закон больших чисел утверждает, что при вероятности события А равной

(причем N и K нам неизвестны), то всегда можно выбрать достаточно большое N, чтобы выполнялось соотношение:

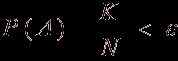
где (ипсилон) - сколь угодно малое положительное неравное нулю число.

Это значит, что при достаточно большом количестве испытаний частота появления того или иного события будет сколь угодно мало отличаться от нуля.

Это соотношение дает возможность устанавливать опытным путем с достаточно хорошим приближением вероятность неизвестного нам события.

3. Задачи и примеры.

Первые расчеты вероятностей событий начались еще в XVII веке с подсчета шансов игроков в азартных играх. В первую очередь это была игра в кости.

Рекомендуем скачать другие рефераты по теме: доклады 7 класс, конспект.



1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки