Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата



, т.к. исходы первого испытания не влияют на исходы второго испытания.  Из факта: P(AB)=P(A)P(B/A); P(B/A)=P(B); AB=EiQj (надо доказать)

A={EiQ1, EiQ2..., EiQj, ..., EiQm2}

B={E1Qj, E2Qj..., EiQj, ..., Em1Qj}

По определению произведения AB в него входят только те события, которые входят и в A, и в B. Из приведенных выше формул следует, что только событие EiQj входит и в A, и в B, то AB= EiQj. Следует:

Композиционное пространство имеет вид: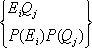

Общая структура независимых событий в композиционном пространстве, порожденном композицией испытаний:

т.е. в результате первого испытания произошли элементарные события: .

В результате второго испытания события: .

Сложное событие B определяет все возможные комбинации исходов двух испытаний независимо друг от друга. В результате первого испытания произошли элементарные события: .

В результате второго испытания события:  .

Тогда:

, т.к. второе испытание не влияет на результаты первого.

т.к. , (надо доказать)

то

При решении практических задач, связанных с независимыми испытаниями обычно не требуется строить композиционных пространств элементарных событий, а использовать формально неверную запись:  P(A×B)=P(A)×P(B).

Композиция n испытаний.

Имеется n испытаний. Зададим для i-го испытания вероятностное пространство:

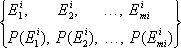        i=1, ..., n

Композицией n испытаний называется сложное испытание, состоящее в совместном проведении n испытаний. Задается n испытаний, вероятностное пространство каждого из которых имеет вид:

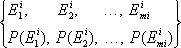          i=1, ..., n

Композиционное пространство имеет вид:

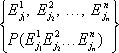                    j1=1, ..., m1;      j2=1, ..., m2;      jn=1, ..., mn;

Рекомендуем скачать другие рефераты по теме: bestreferat, quality assurance design patterns системный анализ.

Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки