Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

A8=(w 1, w 2, w 3)

Обозначим систему этих событий через F. Берем произвольное событие AÎ F. Проводим серию испытаний в количестве n. n - это количество испытаний, в каждом из которых произошло событие A.

Частостью наступления события A в n испытаниях называется число

 

Свойства частости.

Частость достоверного события равна 1. n(U)=1.

Частость суммы попарно несовместных событий равна сумме частостей.

Рассмотрим систему Ai, i=1, ..., k; события попарно несовместны, т.е.

Событие

Пусть в результате некоторого испытания произошло событие A. По определению сумы это означает, что в этом испытании произошло некоторое событие Ai. Так как все события попарно несовместны, то это означает, что никакое другое событие Aj (i¹ j) в этом испытании произойти не может. Следовательно:

nA=nA1+nA2+...+nAk

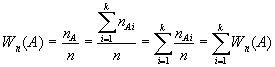
Теория вероятности используется при описании только таких испытаний, для которых выполняется следующее предположение: Для любого события A частость наступления этого события в любой бесконечной серии испытаний имеет один и тот же предел, который называется вероятностью наступления события A.

Следовательно, если рассматривается вероятность наступления произвольного события, то мы понимаем это число следующим образом: это частость наступления события в бесконечной (достаточно длинной) серии испытаний.

К сожалению, попытка определить вероятность как предел частости, при числе испытаний, стремящихся к бесконечности, закончилась неудачно. Хотя американский ученый Мизес создал теорию вероятности, базирующуюся на этом определении, но ее не признали из-за большого количества внутренних логических несоответствий.

Теория вероятности как наука была построена на аксиоматике Колмогорова.

Аксиоматика теории вероятности.

Построение вероятностного пространства.

Последовательно строим вероятностное пространство.

Этап 1:

Имеется испытание. В результате проведения испытания может наблюдаться одно событие из серии событий e . Все события из системы e называются наблюдаемыми. Введем предположение, что если события A Ì e , B Ì e наблюдаемы, то наблюдаемы и события .

Система событий F называется полем событий или алгеброй событий, если для двух произвольных событий A, B Ì F выполняется:

Дополнения

Рекомендуем скачать другие рефераты по теме: изложение по русскому 6 класс, реферат анализ.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки