Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Покажем, что события несовместны.

* Если события несовместны, то ; ;

т.е. события несовместны.

Тогда по третей аксиоме теории вероятности

Справедливо следующее тождество на основании (1) и закона дистрибутивности

Показать самим, что все три множества попарно несовместны.

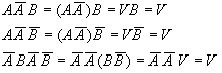
На основании первой и третей аксиомы теории вероятности получаем:

Имеет место тождество , показать самим, что несовместны

По третей аксиоме:

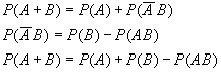
Для экзамена доказать самим формулу суммы произвольного числа событий

Формула полной вероятности.

Рассмотрим систему A из k попарно несовместных событий.

B1, B2, ..., Bk

Пусть дано событие A, удовлетворяющее равенству A=B1A+B2A+...+BkA.

Показать, что события B1A, B2A, BkA попарно несовместны. BiABjA=BiBjAA=VAA=V

Найти вероятность наступления события A. Любое событие входящее в A, обязательно входит в некоторое, но одно Bi, т.к. B1, B2, ..., Bk образуют полную группу.

Т.к. B1, B2, ..., Bk несовместны, то по третей аксиоме теории вероятности имеем:

; т.е.

Рекомендуем скачать другие рефераты по теме: изложение по русскому 6 класс, реферат анализ.



Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки