Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата

.

Так, например, для цикла  в рассмотренной выше задаче имеем

.

Для базисных клеток сумма потенциалов строки и столбца, в которых находится эта клетка, равна тарифу, соответствующему этой клетке; если же клетка для неизвестного  свободная, то сумму потенциалов

(4.2)

называют косвенным тарифом этой клетки. Следовательно, алгебраическая сумма тарифов для свободной клетки  равна разности ее настоящего (“истинного”) и косвенного тарифов:

(4.3)

Из (4.3) следует, что если косвенный тариф для данной свободной клетки больше её истинного тарифа, то алгебраическая сумма тарифов по циклу, соответствующему этой клетке, будет отрицательна; если же косвенный тариф меньше истинного, то алгебраическая сумма тарифов положительна, и, наконец, если косвенный тариф равен истинному, то алгебраическая сумма тарифов равна нулю.

Потенциалы можно найти из системы равенств (4.1), рассматривая их как систему  уравнений с  неизвестными. Так как неизвестных здесь на единицу больше, чем уравнений, то, по крайней мере, один из потенциалов мы можем выбрать произвольно, положив, например, ; тогда остальные потенциалы легко определяются из уравнений (4.1).

Например, для плана, полученного по диагональному методу в рассмотренной выше задаче, имеем

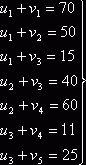
Система содержит семь уравнений с восемью неизвестными. Выбирая произвольно значение , находим последовательно из первых трех уравнений значения , , , затем из четвертого уравнения – , из пятого уравнения – , из шестого уравнения  и, наконец, из седьмого уравнения – .

Положив, например, , получаем значения потенциалов:

 

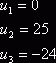
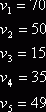
Найдем теперь косвенные тарифы для свободных клеток и сравним их с истинными тарифами:

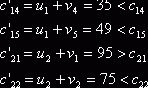
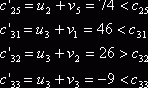
Для клеток с неизвестными  и  косвенные тарифы больше истинных. Следовательно, для них мы будем иметь отрицательные алгебраические суммы тарифов:

Значение  мы уже имели раньше, вычисляя алгебраическую сумму тарифов для этой клетки непосредственно по циклу.

Замечание 1. Подсчитывая косвенные тарифы как суммы соответствующих потенциалов, полезно не пропускать и клетки с базисными неизвестными (заполненные клетки). Для этих клеток сумма потенциалов равна истинному тарифу; последнее может служить проверкой правильности найденных значении потенциалов.

Замечание 2. Можно показать, что если сумму всех затрат по данному плану перевозок выразить через свободные неизвестные [для этого надо исключить базисные неизвестные из выражения для S, см. формулу (2.4)], то коэффициент при каждом из таких неизвестных будет равен алгебраической сумме тарифов по циклу, соответствующему ей в таблице перевозок. Это еще раз подтверждает, что пересчет по циклам является специфической формой применения симплекс-метода к решению транспортной задачи.

Критерий оптимальности базисного решения транспортной задачи. Методы отыскания оптимального решения.

Из сказанного в предыдущем пункте вытекает следующий критерий оптимальности базисного решения транспортной задачи: если для некоторого базисного плана перевозок алгебраические суммы тарифов по циклам для всех свободных клеток неотрицательны, то этот план оптимальный.

Рекомендуем скачать другие рефераты по теме: сайт рефератов, контрольная работа 7.



Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки