Транспортная задача линейного программирования
Категория реферата: Рефераты по математике
Теги реферата: сочинение описание, курсовики скачать бесплатно
Добавил(а) на сайт: Эсмеральда.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
Система (2.1) содержит 
уравнений с 
неизвестными. Её
особенность состоит в том, что коэффициенты при неизвестных всюду равны
единице. Кроме того, все уравнения системы (2.1) могут быть разделены на две
группы: первая группа из т первых уравнений (“горизонтальные” уравнения) и
вторая группа из п остальных уравнений (“вертикальные” уравнения). В каждом из
горизонтальных уравнений содержатся неизвестные с одним и тем же первым
индексом (они образуют одну строку матрицы перевозок), в каждом из вертикальных
уравнений содержатся неизвестные с одним и тем же вторым индексом (они образуют
один столбец матрицы перевозок). Таким образом, каждая неизвестная встречается
в системе (2.1) дважды: в одном и только одном горизонтальном и в одном и
только одном вертикальном уравнениях.
Такая структура системы (2.1) позволяет легко
установить ее ранг. Действительно, покажем, что совокупность неизвестных, образующих первую строку и первый столбец матрицы перевозок, можно принять в
качестве базиса. При таком выборе базиса, по крайней мере, один из двух их
индексов равен единице, а, следовательно, свободные неизвестные определяются
условием 
, 
.Перепишем систему (2.1) в виде
|
(2.1’) |
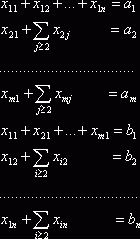
где символы 
и 
означают суммирование по соответствующему индексу. Так, например,
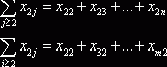
При этом легко заметить, что под символами такого
суммирования объединяются только свободные неизвестные (здесь , ).
В рассматриваемой нами системе только два уравнения, а
именно первое горизонтальное и первое вертикальное, содержат более одного
неизвестного из числа выбранных нами для построения базиса. Исключив из первого
горизонтального уравнения базисные неизвестные 
с помощью вертикальных
уравнений, мы получаем уравнение
или короче
|
(2.2) |
где символ 
означает сумму всех
свободных неизвестных. Аналогично, исключив из первого вертикального уравнения
базисные неизвестные 
с помощью
горизонтальных уравнений, мы получаем уравнение
|
(2.2’) |
Так как для закрытой модели транспортной задачи 
, то полученные нами уравнения (2.2) и (2.2’) одинаковы и, исключив из одного из них неизвестное 
, мы получим уравнение-тождество 0=0, которое из системы
вычеркивается.
Итак, преобразование системы (2.1) свелось к замене
двух уравнений (первого горизонтального и первого вертикального) уравнением
(2.2). Остальные уравнения остаются неизменными. Система приняла вид
|
(2.3) |
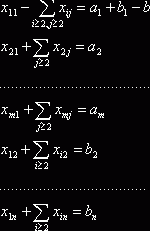
В системе (2.3) выделен указанный выше базис: базисные
неизвестные из первых т уравнений образуют первый столбец матрицы перевозок, а
базисные неизвестные остальных уравнений образуют первую строку матрицы перевозок
без первого неизвестного [она входит в первое
уравнение системы (2.3)]. В системе (2.3) имеется 
уравнений, выделенный
базис содержит неизвестных, а, следовательно, и ранг системы (2.1) 
.
Для решения транспортной задачи необходимо кроме
запасов и потребностей знать также и тарифы 
, т. е. стоимость перевозки единицы груза с базы 
потребителю 
.
Совокупность тарифов также образует
матрицу, которую можно объединить с матрицей перевозок и данными о запасах и
потребностях в одну таблицу:
|
Пункты Отправления Рекомендуем скачать другие рефераты по теме: сайт рефератов, контрольная работа 7. Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |