Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Где - абсолютный интервал t-подобной массы покоя

- относительный интервал t-подобной энергии;

- относительный интервал x-подобного импульса

об абсолютной природе интервала можно говорить лишь в относительном смысле, в связи с применением, так как по аналогии с правой частью равенств 1) и 2), абсолютный интервал в левой части равенства, может быть выражен в форме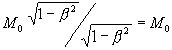. Интервал абсолютен только при.

Поскольку 1/1, 1/ не могут рассматриваться иначе, как равноправные (наравне с), ясно, что масса покоя 1),2) теряет свой абсолютный смысл, если ее рассматривать относительно = 1/ или = 1/1, т.е. представление абсолютности интервала 2) справедливо лишь при.

3.3. Незавершенность геометрии ИСО в СТО. Внутренние (нарушение симметрии в уравнении скоростей, наличие несистемных областей пространства-времени) и внешние (независимость системы отсчета от материи, неточность отражения движения в связи с гравитационными эффектами) противоречия ИСО в СТО, необоснованность выражения пространственно-временного континуума теоремой Пифагора в связи с принципиально различной природой пространства (как протяженной характеристики) и времени (как длительной характеристики), позволяют сделать вывод, что ограниченность ИСО в СТО связана, прежде всего, с незавершенностью, неразвернутостью геометрии ее координатного пространства.

4. ПРЕОБРАЗОВАНИЕ СИСТЕМЫ ОТСЧЕТА МИНКОВСКОГО

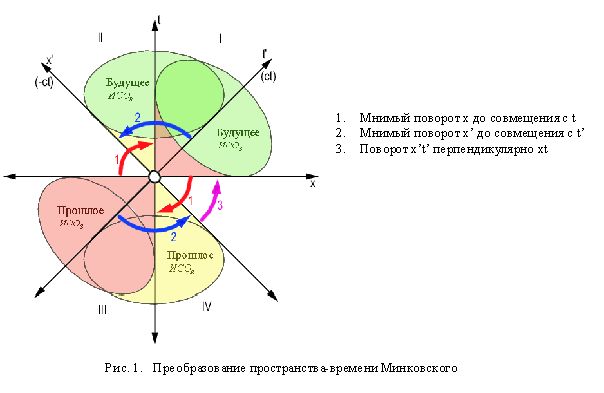
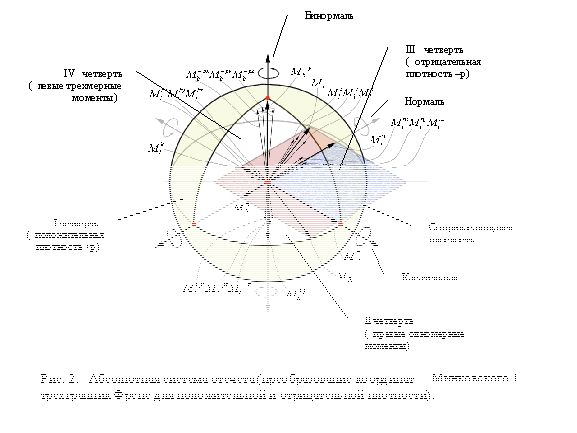
С учетом вышесказанного, преобразование ИСО СТО Минковского, с целью снятия противоречий, предполагает две главных процедуры (рис.1, рис.2):

4.1. Мнимый поворот координатных осей пространства-времени Минковского.

А) Мнимый поворот х-подобной оси х (ИСО СТО) на до совмещения с отрицательной полуосью времени -t (конус прошлого) и превращением ее в отрицательную мнимую величину -iх, противонаправленную времени t (Г.Корн, Т.Корн. Справочник по математике, -М.: Наука, 1973, с.31-33). Закон сохранения (для интервала массы покоя) приобретает следующее выражение:

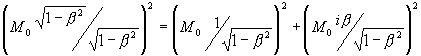3)

Поворот не изменил отношений в формуле 2). Пространственный вектор приобрел отрицательный знак относительно положительного вектора и заменил суммой разность между двумя квадратами относительных интервалов ИСО СТО, но при этом, вошедшая в выражение импульса мнимая единица, вернула нас вновь к разности квадратов интервалов.

Б) Этому повороту соответствует аналогичный поворот и совмещение -ct и ct (далее) и, кроме того, общий поворот совмещенных осей () на в положение, перпендикулярное совмещенным осям (T,iХ), т.е в положение, занимаемое осью пространства ИСО СТО :

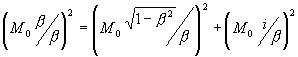4)

Относительный интервал энергии () получил зеркальную, x-подобную форму, относительный интервал импульса (Мо* 1/), наоборот, t-подобную форму, абсолютный интервал Мо* / – x-подобную форму. Взятые относительно светоподобного интервала = 1/1, уравнения приобретают абсолютно идентичную количественную форму с зеркальной метрикой: свойство абсолютного интервала приобретает энергия (x-подобная и t-подобная), абсолютные интервалы в уравнениях 3) и 4) приобретают роль относительных импульсов. Абсолютные, комплексные: t-подобный и x-подобный интервалы энергии связывают в псевдоевклидовой геометрии Минковского пары относительных осевых противоположно направленных импульсов, при этом :

5)

6)

Природа псевдоевклидовой метрики связана с осевым (положительным и отрицательным) направлением относительных импульсов. Абсолютный интервал - комплексная величина. Квадрат абсолютного интервала энергии - полная энергия оси, равная разности квадратов импульсов (при скоростях и i). С учетом мнимой величины, не исключена возможность того, что разность квадратов импульсов в правой части равенства - это разность кинетической и потенциальной энергий. Характерной особенностью уравнений, кроме их зеркальной симметрии, является то, что при действительном и мнимом импульсах, интервал энергии выступает как абсолютный, комплексный, скалярный интервал, но в случае, если мнимый импульс приобретает действительную форму, комплексная энергия приобретает действительную форму и при = =, (прис), ее интервал равен нулю. В ИСО СТО условие равенства относительных интервалов выполняется при =1 (при скорости света). Второй особенностью является то, что из уравнений сохранения (в связи с переходом к = 1/1) , устранены бесконечные величины (уравнения 5), 6)). Кроме того, x-подобные (так же как и t-подобные) полуоси связаны теоремой Пифагора в Евклидовой метрике. При всех значениях разрешенных скоростей осевые и взаимно ортогональны.

4.2. Подвижный трехгранник Френе и пространство кручений. Поскольку вновь образованная, за счет зеркальной симметрии, ИСО уже не может быть связана с поступательным движением (обе ИСО имеют единый центр, и следовательно движение может быть связано с изменением направления скорости, в условиях отсутствия трансляций), поскольку при изменении скоростей координатное пространство не подвержено преобразованиям с кручениями осей подобно ИСО СТО, она может рассматриваться только как вращательная (торсионная) система отсчета, а движение в ней (расширение или сокращение), может рассматриваться как функция изменения состояния пробной массы (объема, плотности). В связи с вышесказанным, ИСО может интерпретироваться как комплексная форма соединения мнимого и действительного “подвижных” трехгранников Френе для случая кручений по направлениям базисных (нормального, касательного, бинормального) векторов. При этом, плоскость векторов нормального и касательного моментов, соответствующая относительным импульсам в и, представляется как соприкасающаяся плоскость, а третий вектор, ортогональный двум указанным – бинормаль, равен векторному произведению нормального и касательного векторов (Г.Корн, Т.Корн. Справочник по математике. – М.: Наука, 1973г., с.521-524).

Характерно, что нормаль (или главная нормаль), касательная и бинормаль – компоненты базисных векторов трехгранника Френе, связаны с кривизной и кручением пространства и лежат в основе тензорного определения кривизны пространства (например, тензоры Риччи второго ранга), примененного А.Эйнштейном в ОТО. В связи с комплексной формой выражения законов сохранения, ИСО представлена тремя (действительным, мнимым и комплексным) трехгранниками Френе. Результатом зеркальной симметрии двух трехгранников, подвижных в противоположных направлениях, является статичная система отсчета, в которой отсутствуют трансляционные координаты (т.е. отсутствует пространство-время). Потеря пространственно-временной определенности – цена перехода к шестимерному пространству кручений. В условиях зеркальной симметрии нормального и касательного базисных векторов, векторное произведение нормальной скорости (мнимой или действительной) на касательную (мнимую или действительную) в инерциальной системе отсчета будет иметь форму квадратов относительных скоростей соответственно = 11, ,.

Таким образом ИСО связана с кручениями, где: 1, и - относительные угловые скорости ; = 11, , - бинормальные (квадратичные) скорости. Импульсы и энергии в законах сохранения, соответственно, являются моментами (инерции) энергий и импульсов. Поскольку в полученной системе отсчета состояние покоя связано с = = или 0,707… скорости света, (при, связанной с массами положительной плотности и при, связанной с массами отрицательной плотности), состояние покоя результирующей системы будет характеризоваться нулевой плотностью покоя. (+p) + (-p) = 0, а сама система отсчета может рассматриваться как абсолютная система отсчета движения изолированной физической системы. Различие в метрике отдельных элементов системы отсчета отражает не отношения пространства и времени, а отношения между 3-мерными и 1-мерными элементами пространства скоростей (в частности нормальные и касательные скорости).

4.3. Уравнения законов сохранения в абсолютной системе отсчета. Геометрия преобразованной системы включает следующие основные законы сохранения (при следующих физических величинах):

Рекомендуем скачать другие рефераты по теме: шпоры по гражданскому, предмет культурологии.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки