Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

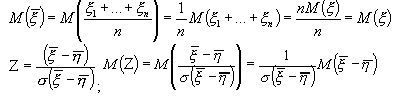
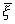- СВ:

Д(Z)- дисперсия Д((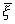- 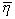)/s (-)) =

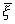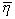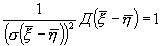
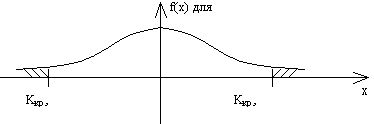
M(Z) = 0; Д(Z) = 1. Для того, чтобы выбрать Zкр. и при заданном уровне значимости a , определить принимается или не принимается основная гипотеза, найти вероятности.

P(0 < Z < Zкр.) + P(Z > Zкр. прав.) = Ѕ Ф(Zкр.) + a /2 = Ѕ Ф(Zкр. прав.) = Ѕ - a /2

Zнабл. =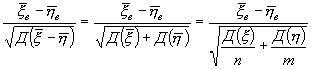

|Zнабл.| < Zкр.прав. Ю Н0 |Zнабл.| > Zкр.прав. Ю Н0 отвергается.

38. Проверка гипотезы о равенстве генеральных средних при неизвестных дисперсиях.

Пусть x и h нормально распределенные СВ, предполагается, что неизвестны, но равны между собой дисперсии. x 1, x 2, ... , x n h 1, h 2, ... , h m

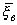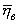; : Н0: М(x ) = М(h ) Н1: М(x ) № М(h )

Для проверки гипотезы Н0, вводится СВ t, которая представляет собой

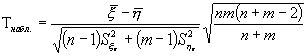
Теоретическое обозначение признака; СВ Т распределена по закону Стъюдента, зависит от первого параметра, который называется числом степеней свободы (k).

k = n + m – 2 (по таблице для распределения Стъюдента при заданном значении k и уровне значимости a в зависимости от вида альтернативной и конкурирующей гипотезы, находятся либо односторонние tкр., либо двухсторонние tкр.).

Ткр. прав. = - Ткр. лев. | Тнабл. | < Ткр. двуст. Ю Н0 | Тнабл. | > Ткр. двуст. Ю Н0 отвергается.

42. Марковские случайные процессы. Размеченный граф состояний.

Предположим, что дана система S. Предп., что состояние этой сис-мы хар-ся параметрами состояний. Если состояние системы меняется во времени случайно, то говорят, что в сис-ме протекает случайный процесс. Сис-ма —аудитория. Для хар-ки состояния используется параметр—число студентов, тогда эта система с дискретными состояниями. Будем рассматривать системы с дискретными состояниями и непрерывным t: сис-ма мгновенно в произвольные сегменты t скачками меняет состояние. Если параметр t принимает дискретные значения (t=1,2,3,...), то происходит процесс с дискретным временем (случайная последовательность), если же t изменяется на некотором интервале, то процесс с непрерывным временем. Если случайные величины семейства принимают дискретные значения, то имеет место процесс с дискретными значениями, если же непрерывное, то с непрерывными значениями. Предположим, что рассматривается система с дискретными состояниями и непрерывным t. Пусть S1, S2,...,Sn —возможные состояния сис-мы. Для описания процесса, происх. в сис-ме, надо знать вер-ти каждого состояния на произвольный момент t. Р1(t)—вер-ть того, что в момент t сис-ма находится в 1-ом состоянии. Процесс, протекающий в системе, наз. марковским, если для него вероятность попасть в состояние Xi=Si в момент ti зависит не от всего прошлого, а лишь от состояния Xi-1=Si, в котором процесс был в предыдущий момент времени ti-1. Графом называется совокупность вершин и дуг, соединяющих эти вершины. Для описания процесса, протекающего в системе, удобно использовать размеченный граф состояний, в котором в кач-ве вершин исп-ся различные состояния системы, а в кач-ве дуг—стрелки, показ. возможные переходы за 1 шаг из состояния в состояние. При этом над каждой стрелкой указ. Плотность вероятности соответствующего перехода.

43. Система дифф. уравнений Колмогорова для вероятностей состояний.

Пусть дан марковский случайный процесс. Рi(t)—вер-ти состояний: i=1,n(все с чертой), тогда для Рi(t) выполняется следующее дифференциальное уравнение

d Рi(t)/dt=е ( от i<>k,k=1 до n) l ki* Рi(t)—е ( от j<>1,j=i до n) l ij*Pi(t); i=1,n(все с чертой) (1) Система из n уравнений , т.к. для любого момента t е ( от i=1 до n) Pi(t), то в системе (1) одно любое уравнение м-но отбросить. И, задав начальное условие на момент t=t0, P1(t0)=1, Pi(t0)=0, i=1,n( все с чертой).

В итоге м-но решить сис-му дифф. ур-ний и найти все вер-ти состояний Pi(t), i=1,n(все с чертой).

44. Предельные вероятности состояний. Нахождение предельных вероятностей.

Предположим, что дан марковский случайный процесс, тогда, используя уравнение Колмогорова, можно найти Рi(t); i =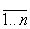

Предельными или финальными вероятностями называют пределы

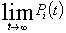, если эти вероятности существуют, т.е. 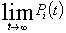= Рi.

Если эти предельные вероятности существуют, то в системе устанавливается стационарный режим, при котором состояние системы меняется случайным образом, но вероятность каждого состояния остается неизменной.

Предельная вероятность в марковском случайном процессе существует, если этот процесс удовлетворяет свойству транзитивности. Процесс в протекающей системе называется транзитивным, если существует интервал времени t , в течение которого система может перейти из любого состояния Si в любое другое состояние Sj.

Алгебраические уравнения для предельной вероятности состояний

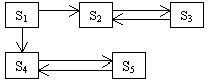
Пусть марковский случайный процесс удовлетворяет свойству транзитивности, тогда для него при t ® Ґ существуют предельные вероятности состояний Pi=const.

Рекомендуем скачать другие рефераты по теме: реферат на тему труд, купить дипломную работу.



Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки