Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

где ,  выписываются явно (i=1,2; j=1,2; k=1..N). Таким образом, получаем:

                            (1.11)

Из первого краевого условия получаем зависимость  от , затем, подставляя во второе краевое условие (1.6), получаем уравнение для собственных значений задачи (1.4)-(1.6):

,                                                         (1.12)

где  выписывается явно.

Пусть  - собственные значения и  - соответствующие им собственные функции задачи (1.4)-(1.6), где через h обозначено

,

и пусть - собственные значения задачи (1)-(3) и  соответствующие им собственные функции. Введем обозначение:

.                                        (1.13)

Заметим прежде, что  при .

Тогда имеет место следующая

ТЕОРЕМА 1.1 Справедливы равенства

,                                               (1.14)

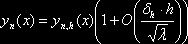.                                        (1.15)

Доказательство. Вначале докажем равенство (1.15). Для этого рассмотрим уравнение (1.1) на интервале . Представим ее в виде

,                                (1.16)

где  вычисляется по формуле (1.7). Для уравнения (1.16) получаем интегральные уравнения:

,

.

Применяя метод последовательных приближений, получаем:

,                       (1.17)

где  - решения уравнения (1.4).

Следовательно, для всего промежутка [0,p] справедливо равенство (1.15).

Из (1.15) нетрудно установить неравенство:

,                           (1.18)

Рекомендуем скачать другие рефераты по теме: конспект урока в школе, дипломы рефераты.



Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки