Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

идею доказательства см. в [1].

Если n=1, вектор порождает неприводимое подпространство в H(p,q). Поскольку Da11S=(p+q)S, этот вектор соответствует старшему весу . Тогда 2x1 - единственный положительный корень, то есть H(p,q) неприводимо.

Пусть n>1. Осталось теперь показать, что

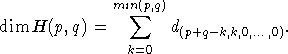
Эту формулу можно доказать по индукции, индуктивный переход делается от пары (p,q) к паре (p+1,q-1), а , что доказывает теорему.

Обозначим через инвариантную относительно вращений положительную борелевскую меру на S4n-1, для которой .

Следствие 1. Пространство является прямой суммой попарно ортогональных пространств P(p,q,r).

Следствие 2. Справедливы утверждения: a) В P(p1,q1,r1) и P(p2,q2,r2) при n>1 реализуются эквивалентные представления тогда и только тогда, когда p1+q1=p2+q2 и r1=r2.

b) При n=1 в H(p1,q2) и H(p2,q2) реализуются эквивалентные представления тогда и только тогда, когда p1+q1=p2+q2.

Пусть Ws,r и Ws - пространства линейных комбинаций векторов и соответственно с комплексными коэффициентами, . Введем также пространства и при n>1.

Следствие 3. Ws,r и Ws - пространства старших векторов неприводимых представлений со старшим весом и s соответственно. Сплетающие операторы неприводимых представлений можно выразить как многочлены от операторов L1 и L2.

Более подробные сведения из теории представлений можно найти, например, в [3].

3. Инвариантные пространства функций на S4n-1.

Пространство Y на сфере S4n-1 назовем инвариантным, если для всех f из Y и всех g из Sp(n) f*g лежит в Y. Неприводимость представления группы Ли Sp(n) эквивалентна неприводимости представления комплексификации ее алгебры Ли sp(n,C), поэтому пространства P(p,q,r) и H(p,q) при n=1 инвариантны.

Если Y - инвариантное замкнутое подпространство , то также инвариантно и ортогональная проекция коммутирует с Sp(n). Это верно также для ортогональных проекций и .

Когда в пространствах V и W реализуются неприводимые представления, пространство сплетающих операторов из V в W либо одномерно (если представления эквивалентны), либо пусто. Отсюда, из следствия 2 теоремы 1 и предложения 1 вытекает

Предложение 3. Пусть n>1 и линейное отображение коммутирует с Sp(n). Тогда

1) если или , то T=0.

2) если r1=r2 и p1+q1=p2+q2, то найдется константа C, такая что при T=CL2p1-p2, при T=CL1p2-p1.

Обозначим через неприводимое инвариантное пространство со старшим вектором , а через -замыкание пространства Y.

Теорема 2. Если Y - замкнутое инвариантное подпространство , то , .

Доказательство. Пусть n>1 и тройка (p,q,r) такая, что . Так как Y инвариантно и коммутирует с Sp(n), то - нетривиальное инвариантное подпространство P(p,q,r). Значит, Пусть и Y1 - ортогональное дополнение к Y0 в Y. Тогда Y0 инвариантно как ядро оператора, коммутирующего с Sp(n), значит Y1 также инвариантно. Более того, - изоморфизм, обратный к которому обозначим

Выберем другую тройку (p',q',r') и рассмотрим отображение Оно коммутирует с Sp(n) и переводит P(p,q,r) в P(p',q',r'). Значит, по предложению 3, для всех (p',q',r'), таких что

Тогда Y1 - подпространство . Рассмотрим и содержащее его минимальное инвариантное пространство, оно совпадает с Y1.

Рекомендуем скачать другие рефераты по теме: доклад листья, шпоры по социологии.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки