Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

где

P(Z) = 1 - dZ-N, Fk(Z) = 1 / (1 - bkZ-1), d = ej2pk, bk = e j2pk/N  (3.11)

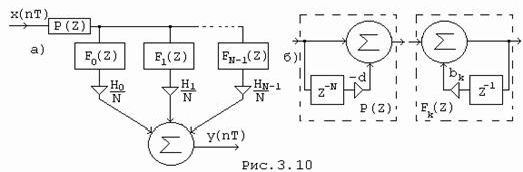
Схема фильтра, соответствующего (3.10), приведена на Рис. 3.10, а. Схемы звеньев фильтра, соответствующих (3.11), приведены на Рис. 3.10, б.

Схема фильтра на рис. 3.10 применяется с учетом поправок, обусловленных особенностями расположения нулей и полюсов передаточной функции.

Нули и полюсы H(Z) (3.10), т.е. корни уравнений

1- ej2pk Z-N = 0, 1 - e j2pk/N Z-1 = 0

Расположены на единичной окружности плоскости Z в точках

Zk = e j2pk/N

и взаимно компенсируется. Но компенсация получается неполной по причине конечной разрядности кодовых слов, что приводит к скачкам частотной характеристики фильтра и, более того, не исключена вероятность самовозбуждения цепи. Поэтому рекомендуется смещать  точки Zk внутрь единичного круга на малую величину, т.е.

Zk = e -aT/N e j2pk/N, где aТ < 10-5

что соответствует коэффициентам фильтра

d = e-aT e j2pk, bk = e-aT e j2pk/N   (3.12)

Небольшая поправка коэффициентов фильтра (3.12) практически не отразится на характеристиках фильтра.

Частотная характеристика фильтра

Частотная характеристика фильтра по методу частотной выборки получается подстановкой

Z = ejwT,

в (3.10). Отсюда, с учетом формулы Эйлера,

H(jw)=  

следовательно

 (3.13)

что соответствует ряду Котельникова для спектров дискретных сигналов. Таким образом, частотную характеристику не рекурсивного ЦФ можно представить как в форме ряда Фурье, так и в форме ряда Котельникова.

Каждая из отсчетных функций в (3.13)

  (3.14)

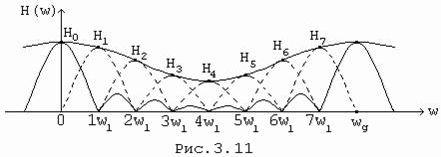
на частоте w = kw1 принимает значение частотной выборки H(jkw1); остальные отсчетные функции на этой частоте обращаются в нуль. На графике Рис. 3.11 показана в качестве примера некоторая АЧХ и ее составляющие - равносмещенные отсчетные функции для случая N=8, где отсчетные функции представлены главным лепестком, кроме модуля отсчетной функции при К=0, которая изображена полностью.

Рекомендуем скачать другие рефераты по теме: информация реферат, доклад по физкультуре.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки