Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

С учетом вышеизложенного становится понятным, что регулировка частотных отсчетов фильтра по методу частотной выборки является взаимонезависимой подобно взаимонезависимой регулировке отсчетов импульсной характеристики не рекурсивного ЦФ по схеме на Рис. 3.2, а.

Расчет фильтра начинается с ориентировочного выбора величины N. Коэффициенты фильтра приравнивают к соответствующим отсчетам требуемой частотной характеристики. Особый случай имеет место в точках разрыва характеристики: отсчеты, расположенные в окрестности точек разрыва, т.е. в переходной области, необходимо выбирать с таким расчетом, чтобы получить удовлетворительное приближение реализованной характеристики к требуемой в диапазоне частот, прилегающем к переходной области. Наиболее часто в переходную область попадает 1 или 2 отсчетных частоты. В этом случае удовлетворительный результат аппроксимации можно получить простым подбором модуля отсчетов в переходной области.

После проверочного расчета частотных характеристик по формуле 3.10 или 3.13 принимается решение о необходимости повторного расчета.

Схема фильтра с вещественными отводами

Реализация фильтров по схеме на Рис. 3.10, а сопряжена с некоторыми особенностями, обусловленными комплексным характером коэффициентов в отводах. Поэтому на практике получил распространение еще один вариант схемы такого фильтра, отличающийся вещественным характером коэффициентов.

Фильтр с вещественными коэффициентами получается за счет объединения каждой пары отводов с индексами К и (N-K), которая является комплексно-сопряженной по причине комплексно-сопряженной симметрии частотных характеристик фильтра относительно частоты 0,5wд. В результате

    (3.15)

где a0k = cos jk, a1k = -bk cos (jk - qk), b1k = -2bk cos qk, b2k = b2k

Схема вещественного отвода, соответствующего (3.15), приведена на Рис. 3.12.

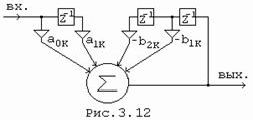
Завершая обсуждение фильтра с частотной выборкой следует отметить еще одно важное качество таких фильтров: в схеме отсутствуют звенья, соответствующие нулевым значениям требуемой АЧХ. В результате, например, схема частотно-селективного фильтра существенно упрощается, сохраняя при этом возможность получения линейной фазы.

Расчет рекурсивных фильтров. Метод билинейного преобразования.

Методы расчета рекурсивных ЦФ можно разделить на прямые и косвенные. Прямые методы предполагают расчет непосредственно рекурсивного ЦФ, косвенные используют в качестве промежуточного этапа расчет аналогового фильтра (АФ).

К числу косвенных методов относится метод билинейного преобразования, основанный на таком преобразовании частот, при котором частотная ось сжимается до конечных размеров. Формула частотного преобразования

 или

где w - реальная частота, т.е. частота проектируемого ЦФ, - расчетная частота, т.е. частота вспомогательного АФ, , - соответствующие комплексные частоты.

На рис. 3.13, а приведен график зависимости расчетной частоты от реальной частоты, на Рис. 3.13, б - пример соответствия кривых АЧХ фильтров АФ и ЦФ.

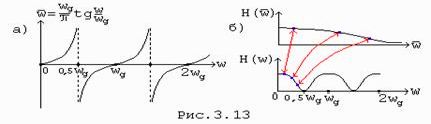
Связь комплексных переменных вспомогательного АФ и реального ЦФ, т.е.  и Z определяется равенством

  (3.17)

Формула (3.17) получается подстановкой в (3.16) Z = epT. В результате

Перечислим последовательность этапов расчета ЦФ методом билинейного преобразования.

1. Перевести требуемые характеристики и нормы ЦФ в соответствующие требования к АФ, применяя формулу

Рекомендуем скачать другие рефераты по теме: информация реферат, доклад по физкультуре.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки