Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Выразим искомую силу численно.

Первое доказательство наличия неуравновешенных сил тяготения внутри сферически-симметричной полости

Определим начальные условия. Пусть задано однородное и изотропное пространство, равномерно заполненное веществом с плотностью равной ρ. Выделим в пространстве сферу радиуса R. Плотность вещества, заполняющего полость сферы, первоначально примем равной нулю. Поместим пробную массу m в центр полости (см. рис.5а).

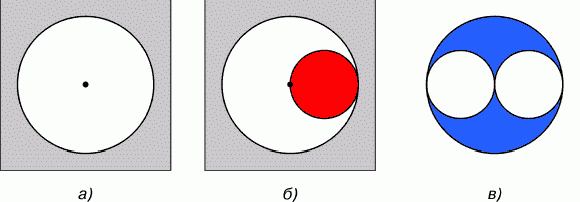
Рис. 5. Неуравновешенные силы тяготения внутри сферически-симметричной полости

Поскольку расположение вещества, находящегося за пределами полости, симметрично относительно центра полости, то сила тяготения, создаваемая всем веществом на пробную массу помещенную в центр полости, будет равна нулю. Внесем внутрь полости массу M, имеющую форму шара радиуса r = R/2.

Положение шара (выделен красным цветом) показано на рис.5б. Плотность вещества, заполняющего объем малого шара, примем равной плотности вещества, окружающего сферу. Согласно закону всемирного тяготения, после помещения внутрь полости пробного тела массой m, на тело будет действовать сила тяготения F.

,

(1)

где G – гравитационная постоянная, M – масса малого шара, m – масса пробного тела, r – расстояние между центром малого шара и пробной массой.

Внесем внутрь полости еще одну массу, имеющую форму фигуры, выделенной на рис.5в синим цветом.

Данная фигура заполняет внутренний объем полости за исключением внесенного шара и его зеркального отражения. Плотность вещества, заполняющего второе тело, также равна плотности вещества, заполняющего окружающее пространство. Отметим, что расположение вещества, заполняющего второе тело, симметрично относительно пробной массы m. Поэтому силы тяготения, создаваемые вторым телом, взаимно уравновешены.

Совместим рис.5б и рис.5в. Получим рис.6а.

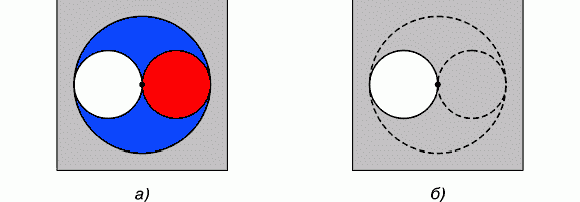
Рис. 6. Расположение вещества, уравновешивающего силы тяготения:

а) пробное тело расположено на краю полости, б) вещество, отмеченное серым цветом, имеет одинаковую плотность

На рис.6б все вещество, имеющее одинаковую плотность, отмечено серым цветом. Граница вещества выделена жирной линией, а условные линии построения сохранены в виде пунктиров.

Пробное тело m расположено на краю только что построенной полости, и на него в данном случае действует сила тяготения (1), созданная малым шаром радиуса r. Сравнение построенной полости с любой другой полостью приводит к выводу, что изменение действия силы на пробную массу может быть вызвано только изменением размеров и плотности окружающего вещества.

Вывод: всякая полость, вне зависимости от природы возникновения, создает силы тяготения в соответствии с формулой (1).

В корректности проведенного доказательства можно убедиться самостоятельно, проделав аналогичные действия с любой другой полостью. Обратим внимание на тот факт, что сила тяготения внутри полости создается не самой полостью (то есть пустотой), а окружающим полость веществом, которое при наличии полости расположено асимметрично по отношению к пробной массе.

Впрочем, приведенное доказательство наличия неуравновешенных сил тяготения внутри сферически-симметричной полости не единственное. Приведем вторую схему рассуждений, которая приводит к тому же результату. Те, кого убедило изложенное, могут перейти к анализу причин ошибочного доказательства отсутствия сил тяготения внутри сферически-симметричной полости.

Второе доказательство наличия неуравновешенных сил тяготения внутри сферически-симметричной полости

На рис.7а показаны две полости равного радиуса R, находящиеся в однородном изотропном пространстве. Плотность вещества, равномерно заполняющего пространство, примем равным ρ. Плотность вещества внутри каждой полости первоначально примем равной нулю.

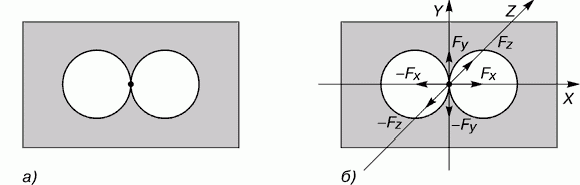
Рис. 7. Две полости в однородном изотропном пространстве

Рекомендуем скачать другие рефераты по теме: конспект урока по русскому языку, решебник по геометрии класс атанасян.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки