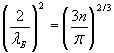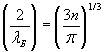–ö–į–ļ –≤–ł–ī–Ĺ–ĺ –ł–∑ —ā–į–Ī–Ľ–ł—Ü—č, –§–í, —Ä–į–≤–Ĺ–į—Ź –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—é —ć–Ĺ–Ķ—Ä–≥–ł–ł —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–į –Ĺ–į –Ņ–Ľ–ĺ—Č–į–ī—Ć —Ā—Ą–Ķ—Ä—č —Ā —Ä–į–ī–ł—É—Ā–ĺ–ľ, —Ä–į–≤–Ĺ—č–ľ
–ĺ—Ä–Ī–ł—ā–į–Ľ—Ć–Ĺ–ĺ–ľ—É —Ä–į–ī–ł—É—Ā—É —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–į, –ł–ľ–Ķ–Ķ—ā –≤–Ņ–ĺ–Ľ–Ĺ–Ķ —Ź—Ā–Ĺ—č–Ļ —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ. –≠—ā–į
–≤–Ķ–Ľ–ł—á–ł–Ĺ–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–ĺ–≤, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć
—Ä–į–∑–ľ–Ķ—Č–Ķ–Ĺ—č –Ĺ–į —ā–ĺ–ľ –ł–Ľ–ł –ł–Ĺ–ĺ–ľ —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ĺ–ľ —É—Ä–ĺ–≤–Ĺ–Ķ. –ö–į–ļ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ —ć—ā–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —Ä–į–≤–Ĺ–ĺ
2n2, –≥–ī–Ķ n ‚Äď –Ĺ–ĺ–ľ–Ķ—Ä —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —É—Ä–ĺ–≤–Ĺ—Ź —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ĺ–ĺ–Ļ –ĺ—Ä–Ī–ł—ā—č.
–ě–ī–Ĺ–į–ļ–ĺ –ĺ—ā –ĺ–Ī—Č–Ķ–Ņ—Ä–ł–Ĺ—Ź—ā–ĺ–≥–ĺ
–Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź –ĺ–Ī —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–ł —Ä–į–ī–ł—É—Ā–į —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ĺ—č—Ö –ĺ—Ä–Ī–ł—ā, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł—Ö –Ī–ĺ–Ľ—Ć—ą–ł–ľ
—ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–ľ —É—Ä–ĺ–≤–Ĺ—Ź–ľ, —Ā–ļ–ĺ—Ä–Ķ–Ķ –≤—Ā–Ķ–≥–ĺ, –Ĺ–į–ī–ĺ –ĺ—ā–ļ–į–∑–į—ā—Ć—Ā—Ź. –ė–∑ –ĺ–Ņ—č—ā–Ĺ—č—Ö –ī–į–Ĺ–Ĺ—č—Ö
–ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ —Ä–į–∑–ľ–Ķ—Ä—č –į—ā–ĺ–ľ–ĺ–≤ –Ĺ–Ķ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź—é—ā —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–į–ľ –Ĺ–į—Ö–ĺ–ī–ł—ā—Ć—Ā—Ź –Ĺ–į —Ā—ā–ĺ–Ľ—Ć
–ĺ—ā–ī–į–Ľ–Ķ–Ĺ–Ĺ—č—Ö —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź—Ö –ĺ—ā —Ź–ī—Ä–į.
–Ě–į –ĺ—Ā–Ĺ–ĺ–≤–Ķ –ī–į–Ĺ–Ĺ—č—Ö
–Ņ—Ä–ł–≤–ĺ–ī–ł–ľ–ĺ–Ļ –≤—č—ą–Ķ —ā–į–Ī–Ľ–ł—Ü—č, –ľ–ĺ–∂–Ĺ–ĺ —Ā–ī–Ķ–Ľ–į—ā—Ć –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ, —á—ā–ĺ –ļ–ĺ–Ĺ—Ā—ā–į–Ĺ—ā–Ĺ–ĺ–Ļ
–≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ, –Ķ–ī–ł–Ĺ–ĺ–Ļ –ī–Ľ—Ź –≤—Ā–Ķ—Ö —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ĺ—č—Ö —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —É—Ä–ĺ–≤–Ĺ–Ķ–Ļ, —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ
—ć–Ĺ–Ķ—Ä–≥–ł–ł –ĺ–ī–Ĺ–ĺ–≥–ĺ —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–į –Ĺ–į –ł—Ö –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–Ķ–Ķ
–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–ľ—É —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ĺ–ľ—É —É—Ä–ĺ–≤–Ĺ—é. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ľ—č –≤—č—Ö–ĺ–ī–ł–ľ –Ĺ–į
–Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –ĺ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–ł –≤ –ļ–į–∂–ī–ĺ–ľ –į—ā–ĺ–ľ–Ķ –ĺ–ī–Ĺ–ĺ–Ļ –ł–Ľ–ł –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ł—Ö
–ł–∑–ĺ—ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–Ķ–Ļ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ —Ā–Ľ–Ķ–ī—É–Ķ—ā –ĺ—ā–Ĺ–Ķ—Ā—ā–ł –ļ –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ
—Ā–ĺ—Ö—Ä–į–Ĺ—Ź—é—Č–ł–ľ—Ā—Ź —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–ľ –≤–Ķ–Ľ–ł—á–ł–Ĺ–į–ľ.
–ü–ĺ –≤—Ā–Ķ–Ļ –≤–ł–ī–ł–ľ–ĺ—Ā—ā–ł, —ć—ā–į
–Ĺ–ĺ–≤–į—Ź –Ĺ–Ķ —Ā–ĺ–≤—Ā–Ķ–ľ –Ņ—Ä–ł–≤—č—á–Ĺ–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā —ā–Ķ –≤–Ĺ–Ķ—ą–Ĺ–ł–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ
–Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –į—ā–ĺ–ľ–į –ł–Ľ–ł –ľ–ĺ–Ľ–Ķ–ļ—É–Ľ—č (–Ĺ–Ķ –ĺ–Ī—Ź–∑–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –Ņ–ĺ —Ą–ĺ—Ä–ľ–Ķ), –Ĺ–į
–ļ–ĺ—ā–ĺ—Ä—č—Ö —Ä–į–∑–ľ–Ķ—Č–į—é—ā—Ā—Ź —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ—č –≤—Ā–Ķ—Ö –ł–Ľ–ł –ĺ—ā–ī–Ķ–Ľ—Ć–Ĺ—č—Ö —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —É—Ä–ĺ–≤–Ĺ–Ķ–Ļ. –Ę–ĺ–≥–ī–į
–ł–∑–ĺ—ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–į—Ź –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā—Ć –į—ā–ĺ–ľ–į, –Ķ—Ā–Ľ–ł –ĺ–Ĺ–į –ĺ–ī–Ĺ–į (–ł–Ľ–ł, –Ľ—É—á—ą–Ķ —Ā–ļ–į–∑–į—ā—Ć, –Ķ–ī–ł–Ĺ–į)
–≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–Ķ–Ķ –≤—Ā–Ķ–≥–ĺ –ī–ĺ–Ľ–∂–Ĺ–į –≤—č—Ā—ā—É–Ņ–į—ā—Ć –≤ —Ä–ĺ–Ľ–ł –ļ–ĺ–Ĺ—Ā—ā–į–Ĺ—ā—č, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—Č–Ķ–Ļ —Ā–≤–ĺ–ł
—Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–Ķ–Ļ, –Ĺ–į–Ņ–ĺ–ī–ĺ–Ī–ł–Ķ —Ä–į–Ĺ–Ķ–Ķ —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–Ĺ—č—Ö. –ß–į—Ā—ā—Ć
—Ā–ł—Ā—ā–Ķ–ľ–Ĺ—č—Ö —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ļ, –ł–Ľ–Ľ—é—Ā—ā—Ä–ł—Ä—É—é—Č–ł—Ö —ć—ā—É –ľ—č—Ā–Ľ—Ć, –ľ–ĺ–∂–Ĺ–ĺ –≤–ł–ī–Ķ—ā—Ć –Ĺ–į —Ä–ł—Ā. 5.
–ü–ĺ–ī–ĺ–Ī–Ĺ—č–Ķ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –≤
–į—ā–ĺ–ľ–Ĺ—č—Ö —Ā—ā—Ä—É–ļ—ā—É—Ä–į—Ö –ī–Ľ—Ź —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–ĺ–≤ —Ā –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ —ć–Ĺ–Ķ—Ä–≥–ł–Ķ–Ļ (–Ņ—Ä–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ, —Ä–į–≤–Ĺ–ĺ–Ļ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–ľ—É –Ĺ—É–Ľ—é) –Ņ—Ä–Ķ–ī—Ā–ļ–į–∑–į–Ĺ—č –ł —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—é—ā—Ā—Ź –≤ –ļ–≤–į–Ĺ—ā–ĺ–≤–ĺ–Ļ –ľ–Ķ—Ö–į–Ĺ–ł–ļ–Ķ —É–∂–Ķ
–ī–į–≤–Ĺ–ĺ. –≠—ā–ĺ—ā —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–Ļ —É—Ä–ĺ–≤–Ķ–Ĺ—Ć –Ĺ–į–∑–≤–į–Ĺ —É—Ä–ĺ–≤–Ĺ–Ķ–ľ –§–Ķ—Ä–ľ–ł, –į —Ā–į–ľ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā—Ć -
–Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā—Ć—é –§–Ķ—Ä–ľ–ł.
–ė–∑ —ć–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā–ĺ–≤
–ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ —Ā —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ–ľ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–į —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–ĺ–≤ –Ĺ–į –≤–Ĺ–Ķ—ą–Ĺ–Ķ–Ļ —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ĺ–ĺ–Ļ
–ĺ–Ī–ĺ–Ľ–ĺ—á–ļ–Ķ –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–ī–ł—ā —É–ľ–Ķ–Ĺ—Ć—ą–Ķ–Ĺ–ł–Ķ –Ķ–Ķ –Ņ–Ľ–ĺ—Č–į–ī–ł (—Ā–≤–ĺ–Ķ–ĺ–Ī—Ä–į–∑–Ĺ–ĺ–Ķ —Ā–∂–į—ā–ł–Ķ), –į —Ā —Ä–ĺ—Ā—ā–ĺ–ľ
–Ņ–ĺ—Ä—Ź–ī–ļ–ĺ–≤—č—Ö –Ĺ–ĺ–ľ–Ķ—Ä–ĺ–≤ –į—ā–ĺ–ľ–ĺ–≤ –Ĺ–į–Ī–Ľ—é–ī–į–Ķ—ā—Ā—Ź –Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ –ł—Ö –≤ —Ä–į–∑–ľ–Ķ—Ä–į—Ö.
–ü—Ä–ł —ć—ā–ĺ–ľ, —Ā—É–ī—Ź –Ņ–ĺ –≤—Ā–Ķ–ľ—É, –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ —Ā—É–ľ–ľ–į—Ä–Ĺ–ĺ–Ļ —ć–Ĺ–Ķ—Ä–≥–ł–ł —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–ĺ–≤ –Ĺ–į –Ņ–Ľ–ĺ—Č–į–ī—Ć
—ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ĺ–ĺ–Ļ –ĺ–Ī–ĺ–Ľ–ĺ—á–ļ–ł, –≤ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ—č—Ö –Ņ—Ä–Ķ–ī–Ķ–Ľ–į—Ö, –ĺ—Ā—ā–į–Ķ—ā—Ā—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ —Ā–ĺ—Ö—Ä–į–Ĺ—Ź—é—Č–Ķ–Ļ—Ā—Ź.
–ü–ĺ—ć—ā–ĺ–ľ—É, –≤–Ņ–ĺ–Ľ–Ĺ–Ķ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ, —á—ā–ĺ –ł–∑–ĺ—ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–į—Ź –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā—Ć —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–į–ļ–∂–Ķ –ł
–ļ–≤–į–Ĺ—ā—É–Ķ–ľ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ –≤ –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ–ĺ–ľ –Ĺ–į–ľ–ł –Ņ–ĺ–Ĺ–ł–ľ–į–Ĺ–ł–ł.
–ě—á–Ķ–Ĺ—Ć –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ, —á—ā–ĺ —ā–į–ļ
–Ĺ–į–∑—č–≤–į–Ķ–ľ—č–Ķ —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ—č –į—ā–ĺ–ľ–į, —Ā —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–ĺ—á–ļ–ł –∑—Ä–Ķ–Ĺ–ł—Ź, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā —Ā–ĺ–Ī–ĺ–Ļ
—Ā–≤–ĺ–Ķ–ĺ–Ī—Ä–į–∑–Ĺ—č–Ķ –ľ–ĺ–ī—č –ļ–ĺ–Ľ–Ķ–Ī–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –ī–≤–ł–∂–Ķ–Ĺ–ł–Ļ, —Ā—É—Č–Ķ—Ā—ā–≤—É—é—Č–ł–Ķ –≤—Ā–Ķ–≥–ĺ –Ľ–ł—ą—Ć –Ĺ–į –ĺ–ī–Ĺ–ĺ–Ļ –ł–Ľ–ł
–Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ł—Ö (–Ĺ–Ķ–ľ–Ĺ–ĺ–≥–ł—Ö) –Ņ—É–∑—č—Ä–Ķ–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č—Ö –ł–∑–ĺ—ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ĺ—č—Ö –ĺ–Ī–ĺ–Ľ–ĺ—á–ļ–į—Ö
–į—ā–ĺ–ľ–į. –ü–ĺ-–≤–ł–ī–ł–ľ–ĺ–ľ—É, —ć—ā–ł –ł–∑–ĺ—ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ĺ—č–Ķ –ĺ–Ī–ĺ–Ľ–ĺ—á–ļ–ł –ľ–ĺ–≥—É—ā –ł–ľ–Ķ—ā—Ć
–ľ–Ĺ–ĺ–≥–ĺ–Ľ–Ķ–Ņ–Ķ—Ā—ā–ļ–ĺ–≤—č–Ļ –≤–ł–ī –ł–Ľ–ł —Ä–į–∑–ľ–Ķ—Č–į—ā—Ć—Ā—Ź –ĺ–ī–Ĺ–į –≤ –ī—Ä—É–≥–ĺ–Ļ - –Ĺ–į–Ņ–ĺ–ī–ĺ–Ī–ł–Ķ –ľ–į—ā—Ä–Ķ—ą–Ķ–ļ. –í–ĺ
–≤—Ā—Ź–ļ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ, –ļ–ĺ–ľ–Ņ—Ć—é—ā–Ķ—Ä–Ĺ—č–Ķ –ľ–ĺ–ī–Ķ–Ľ–ł, –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–Ĺ—č–Ķ –Ĺ–į —Ä–Ķ—ą–Ķ–Ĺ–ł–ł —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ –®—Ä–Ķ–ī–ł–Ĺ–≥–Ķ—Ä–į, –ī–į—é—ā –Ņ—Ä–ł–ľ–Ķ—Ä–Ĺ–ĺ —ā–į–ļ–ł–Ķ –ļ–į—Ä—ā–ł–Ĺ—č.
–ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–ĺ
–ł–∑–ĺ—ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–ľ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–Ĺ—č–ľ –≤–Ķ–Ľ–ł—á–ł–Ĺ–į–ľ –≤ –ľ–ł–ļ—Ä–ĺ–ľ–ł—Ä–Ķ –≤–Ņ–ĺ–Ľ–Ĺ–Ķ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ
—Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–Ķ –ł –ł–∑–ĺ–ł–ľ–Ņ—É–Ľ—Ć—Ā–Ĺ—č—Ö –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ. –ü–ĺ –ļ—Ä–į–Ļ–Ĺ–Ķ–Ļ –ľ–Ķ—Ä–Ķ, –Ĺ–į
–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ā–į–ļ–ł—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ —É–ļ–į–∑—č–≤–į–Ķ—ā —Ā–ł—Ā—ā–Ķ–ľ–į –§–í.
–Ę–Ķ–Ņ–Ķ—Ä—Ć –ĺ—ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ļ
–ĺ–Ī –ł–∑–ĺ—ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –ł –ł–∑–ĺ–ł–ľ–Ņ—É–Ľ—Ć—Ā–Ĺ—č—Ö –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–Ĺ—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ–į—Ö –≤–Ķ—Ä–Ĺ–Ķ–ľ—Ā—Ź –ļ –Ī–ĺ–Ľ–Ķ–Ķ
–Ņ—Ä–ł–≤—č—á–Ĺ—č–ľ –§–í, –≤ —ā–ĺ–ľ —á–ł—Ā–Ľ–Ķ –ļ –≤–ĺ–Ľ–Ĺ–Ķ –ī–Ķ –Ď—Ä–ĺ–Ļ–Ľ—Ź.
–í –ļ–≤–į–Ĺ—ā–ĺ–≤–ĺ–Ļ –ľ–Ķ—Ö–į–Ĺ–ł–ļ–Ķ
–ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā—Ā—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź –ĺ–Ī —ć–Ĺ–Ķ—Ä–≥–ł–ł –§–Ķ—Ä–ľ–ł, –į —ā–į–ļ–∂–Ķ –ĺ–Ī –ł–ľ–Ņ—É–Ľ—Ć—Ā–Ķ, —Ā–ļ–ĺ—Ä–ĺ—Ā—ā–ł –ł
—ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ –§–Ķ—Ä–ľ–ł. –ě–ī–Ĺ–į–ļ–ĺ —Ā–ĺ–≤—Ā–Ķ–ľ –Ĺ–Ķ —É–Ņ–ĺ—ā—Ä–Ķ–Ī–Ľ—Ź–Ķ—ā—Ā—Ź —ā–Ķ—Ä–ľ–ł–Ĺ ‚Äú–ī–Ľ–ł–Ĺ–į –≤–ĺ–Ľ–Ĺ—č –§–Ķ—Ä–ľ–ł‚ÄĚ.
–•–ĺ—ā—Ź —ć—ā–ĺ—ā —ā–Ķ—Ä–ľ–ł–Ĺ, –Ņ–ĺ –Ĺ–į—ą–ł–ľ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź–ľ, –ī–ĺ–Ľ–∂–Ķ–Ĺ –Ī—č—ā—Ć –Ņ–Ķ—Ä–≤–ł—á–Ķ–Ĺ —Ā—Ä–Ķ–ī–ł –ī—Ä—É–≥–ł—Ö
–Ņ–ĺ–Ĺ—Ź—ā–ł–Ļ. –ü–ĺ —Ā—É—ā–ł, –ľ—č –≥–ĺ–≤–ĺ—Ä–ł–ľ –ĺ —ā–ĺ–Ļ –∂–Ķ –≤–ĺ–Ľ–Ĺ–Ķ –ī–Ķ –Ď—Ä–ĺ–Ļ–Ľ—Ź.
–≠–Ĺ–Ķ—Ä–≥–ł—Ź –§–Ķ—Ä–ľ–ł –Ņ—Ä–ł
–į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–ľ –Ĺ—É–Ľ–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –ł–∑–≤–Ķ—Ā—ā–Ĺ—č–ľ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ–ľ:
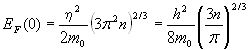 . (6.1)
. (6.1)
–ü—Ä–ł–≤—č—á–Ĺ—č–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–ĺ–ľ
–Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–Ķ–ľ —ć—ā–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ —Ā –≤—č—Ź–≤–Ľ–Ķ–Ĺ–ł–Ķ–ľ –ī–Ľ–ł–Ĺ—č –≤–ĺ–Ľ–Ĺ—č –ī–Ķ –Ď—Ä–ĺ–Ļ–Ľ—Ź, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–Ķ–Ļ
—ć—ā–ĺ–Ļ —ć–Ĺ–Ķ—Ä–≥–ł–ł:
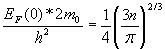
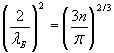
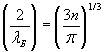
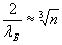 . (6.2)
. (6.2)
–ē—Ā–Ľ–ł —ć–Ĺ–Ķ—Ä–≥–ł—Ź –§–Ķ—Ä–ľ–ł
–Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ—É—é —ć–Ĺ–Ķ—Ä–≥–ł—é —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–ĺ–≤, —ā–ĺ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–į—Ź —ć—ā–ĺ–Ļ
—ć–Ĺ–Ķ—Ä–≥–ł–ł –ī–Ľ–ł–Ĺ–į –≤–ĺ–Ľ–Ĺ—č –ī–Ķ –Ď—Ä–ĺ–Ļ–Ľ—Ź (–ļ–ĺ—ā–ĺ—Ä—É—é –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–∑—č–≤–į—ā—Ć –ī–Ľ–ł–Ĺ–ĺ–Ļ –≤–ĺ–Ľ–Ĺ—č –§–Ķ—Ä–ľ–ł), –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ–ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—É—é –ł–∑ –≤—Ā–Ķ—Ö –≤–ĺ–Ľ–Ĺ, –Ņ—Ä–ł—Ā—É—Č–ł—Ö –ī–į–Ĺ–Ĺ–ĺ–Ļ
—Ā–ĺ–≤–ĺ–ļ—É–Ņ–Ĺ–ĺ—Ā—ā–ł —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–ĺ–≤. –≠—ā–į –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ–į—Ź –ī–Ľ–ł–Ĺ–į –≤–ĺ–Ľ–Ĺ—č (–≤–Ķ—Ä–Ĺ–Ķ–Ķ –Ķ–Ķ –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ–į)
–Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –Ľ–ł—ą—Ć –ĺ–Ī—ä–Ķ–ľ–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā—Ć—é —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–ĺ–≤.
–≠—ā–ĺ—ā —Ą–į–ļ—ā –≤–Ķ—Ā—Ć–ľ–į
–Ņ—Ä–ł–ľ–Ķ—á–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ļ ‚Äď –ĺ–ļ–į–∑—č–≤–į–Ķ—ā—Ā—Ź, –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ–į—Ź –ī–Ľ–ł–Ĺ–į –≤–ĺ–Ľ–Ĺ—č –Ĺ–Ķ –∑–į–≤–ł—Ā–ł—ā –Ĺ–ł –ĺ—ā –ľ–į—Ā—Ā—č, –Ĺ–ł –ĺ—ā —Ā–ļ–ĺ—Ä–ĺ—Ā—ā–ł, –Ĺ–ł –ĺ—ā —á–Ķ–≥–ĺ-–Ľ–ł–Ī–ĺ –ł–Ĺ–ĺ–≥–ĺ, –ļ—Ä–ĺ–ľ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł
–į–Ĺ—Ā–į–ľ–Ī–Ľ—Ź –ľ–ł–ļ—Ä–ĺ—á–į—Ā—ā–ł—Ü.
–•–ĺ—Ä–ĺ—ą–ĺ, –į —á—ā–ĺ –ľ—č –ľ–ĺ–∂–Ķ–ľ
—Ā–ļ–į–∑–į—ā—Ć –ĺ –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ –ī–Ľ–ł–Ĺ–Ķ –≤–ĺ–Ľ–Ĺ—č –ī–Ķ –Ď—Ä–ĺ–Ļ–Ľ—Ź? –†–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –§–Ķ—Ä–ľ–ł-–Ē–ł—Ä–į–ļ–į
–ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā –Ĺ–į–Ľ–ł—á–ł–Ķ –ľ–Ķ–Ĺ—Ć—ą–ł—Ö –ł —Ā–ĺ–≤—Ā–Ķ–ľ –ľ–į–Ľ—č—Ö, –ī–į–∂–Ķ –Ĺ—É–Ľ–Ķ–≤–ĺ–≥–ĺ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź, —ć–Ĺ–Ķ—Ä–≥–ł–ł
—ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–ĺ–≤. –Ę–į–ļ–ł–Ķ –∂–Ķ –ľ–Ķ–Ĺ—Ć—ą–ł–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź, –Ņ–ĺ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é —Ā –ł–ľ–Ņ—É–Ľ—Ć—Ā–ĺ–ľ –§–Ķ—Ä–ľ–ł, –Ī—É–ī—É—ā
–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ī—Ä—É–≥–ł—Ö –ł–ľ–Ņ—É–Ľ—Ć—Ā–ĺ–≤ –ł –≤–ĺ–Ľ–Ĺ–ĺ–≤—č—Ö –≤–Ķ–ļ—ā–ĺ—Ä–ĺ–≤.
–†–Ķ–ļ–ĺ–ľ–Ķ–Ĺ–ī—É–Ķ–ľ —Ā–ļ–į—á–į—ā—Ć –ī—Ä—É–≥–ł–Ķ —Ä–Ķ—Ą–Ķ—Ä–į—ā—č –Ņ–ĺ —ā–Ķ–ľ–Ķ: –ĺ—ā—á–Ķ—ā –Ņ–ĺ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ –Ņ—Ä–į–ļ—ā–ł–ļ–Ķ, —Ā–ĺ—á–ł–Ĺ–Ķ–Ĺ–ł—Ź –Ņ–ĺ –ļ–į—Ä—ā–ł–Ĺ–į–ľ.–ü—Ä–Ķ–ī—č–ī—É—Č–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į —Ä–Ķ—Ą–Ķ—Ä–į—ā–į |
5
6
7
8
9
10
11
12
13
14
15 |
–°–Ľ–Ķ–ī—É—é—Č–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į —Ä–Ķ—Ą–Ķ—Ä–į—ā–į

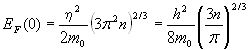 . (6.1)
. (6.1)