Рефераты | Рефераты по науке и технике | Лекции по статистике Лекции по статистике Категория реферата: Рефераты по науке и технике Теги реферата: темы рефератов по информатике, темы докладов по обж Добавил(а) на сайт: Муравьёв. Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 p1

p2

.....

pk

По теоретическому распределению Р можно построить так называемое выравнивающие или теоретические частоты 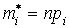. Если отличия между теоретическими и эмпирическими частотами небольшое, то можно считать, что Х распределен по закону Р.

критерий согласия Пирсона

Объективную оценку близости эмпирических частот к теоретическим можно получить с помощью определенных критериев близости, называемых критериями согласия. Существует множество таких критериев. Критерий Пирсона основан на следующем:

.

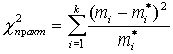Существуют значения (табличные) для соответствующего числа степеней свободы К и уровня значимости 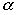. По таблице находятся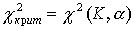

K=k-1-r, где r - число общих характеристик теоретического распределения, принятых равными соответствующим эмпирическим.

11.Оценивание параметров распределений по выборке. Доверительные интервалы.

1. требования к оценкам

Пусть требуется изучить количественный признак генеральной совокупности. Допустим из теоретических соображений удалось установить какое именно распределение имеет признак. Естественна задача оценки параметров этого распределения.

Требования к оценкам:

несмещенность или асимптотическая несмещенность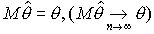

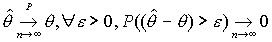
состоятельность

Требование состоятельности применяется к большим объемам.

эффективность

Эффективной называют оценку, которая при заданном объеме выборки n имеет min дисперсию.

надежность оценок

Оценку, определяемую одним числом называют точечной. При выборках малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольших объемах выборки пользуются интервальными оценками, которые определяются 2 числами - концами интервала. Эти оценки позволяют установить точность и надежность оценок.

Пусть 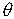=const, 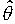тем точнее определяет 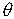, чем меньше (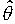-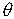). Если есть величина 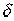>0, (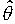-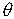)<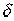, то чем меньше 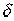, тем точнее оценка.

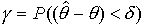- надежность оценки. Обычно надежность задается наперед 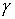=95-99%. Величину 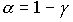называют уровнем значимости.

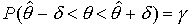, интервал 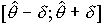- доверительный. Концы этого интервала - случайные величины и называются доверительными границами, они могут меняться от выборки к выборке. Говорят, что наш доверительный интервал с вероятностью 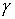покрывает .

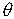Скачали данный реферат: Shelygin, Jabloncev, Федот, Элефтеров, Типалов, Stoljarov.
Последние просмотренные рефераты на тему: гражданин реферат, реферат анализ, реферат по обже, реферат по русскому языку.



Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13

Поделитесь этой записью или добавьте в закладки