Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

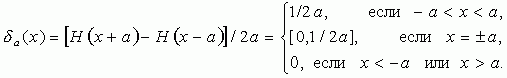 (1.4)

При любом значении a существует интеграл

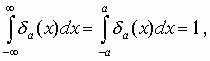
и предел формулы (1.4) при a- 0 является d -функцией, т.е.

 (1.5)

Так определенная (1.4)-(1.5) d -функция является пределом непрерывного графика прямоугольного импульса высотой 1/2a и шириной 2a. При a- 0 высота "стенок" прямоугольного импульса неограниченно возрастает, а ширина импульса стремится к 0. В пределе "стенки" "слипаются" в один луч - d -функцию, расположенную в начале координат.

При прохождении функции в d a(x) по направлению кривой от к "стенки" прямоугольного импульса проходят в противоположных направлениях, поэтому d -функция (состоящая из двух "слипшихся" "стенок") одновременно направлена в противоположных направлениях. (Одну кривую, которую проходят в разных направлениях, считают различными кривыми [8]).

Определенная выше d -функция имеет наглядное представление в виде луча - положительной полуоси ординат. Имея бесконечную высоту и нулевую ширину, d -функция ограничивает единичную площадь (неопределенность типа) и обладает двойной направленностью.

Следует отметить, что в приведенном определении d -функция не рассматривается как "равная нулю при всех и обращающаяся в точке x=0 в бесконечность" [8]. Теперь d -функция рассматривается как луч - линейное множество, имеющее мощность континуума.

Поскольку уточненное определение d -функции не затрагивает ее определения как функционала на пространстве D, все свойства d -функции, рассматриваемой как сингулярная обобщенная функция, сохраняются.

Производная d -функции имеет наглядное представление в виде оси ординат, обладает двойной направленностью в каждой из полуплоскостей y0 и пересекает ось абсцисс (все это в одной точке x=0).

Далее все производные понимаются в обобщенном смысле [6-9], т.е. в виде свертки с производными сингулярной d -функции.

Теория обобщенных функций и разработанная техника вычислений их производных [6-9] позволяют распространить необходимые условия экстремума на континуально многозначные (так называемые разрывные) функции многих действительных переменных.

2. Вариационные задачи с разрывным интегрантом

Многие прикладные оптимизационные задачи сводятся к поиску экстремумов интегральных функционалов с разрывным интегрантом. Здесь "разрывной" понимается так: не обязательно разрывной. Обычно, в том числе и в монографиях [3, 5], оптимизационные задачи рассматриваются для функционалов, зависящих от операторов дифференцирования. В работах [10, 11] рассматриваются функционалы, зависящие от интегральных операторов, что существенно расширяет круг решаемых задач.

Будем решать вариационную задачу для функционалов с разрывным интегрантом, зависящих от линейных интегральных операторов

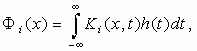 (2.1)

где h(t) - экстремаль, относительно которой предполагаем, что.

Функционал качества I может зависеть от нескольких операторов

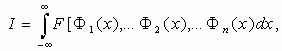 (2.2)

где F[T ]- интегрант, определяющий связь (композицию) операторов F i в функционале I. Интегрант F[T ] может быть непрерывным, гладким, негладким и даже континуально многозначным или разрывным.

Оптимизации методами негладкого анализа посвящена монография Френка Кларка [3], но методику Кларка применить к функционалам, зависящим от интегральных операторов, нельзя, как нельзя ее применять и для функционалов с континуально многозначным или разрывным интегрантом. Кроме того, экстремали у Кларка предполагаются абсолютно непрерывными. Все это несколько сужает область применения негладкой оптимизации Кларка - теории, впитавшей в себя достижения его предшественников, на кoторых он ссылается в своей монографии. Поскольку оптимизируемый функционал зависит от интегральных операторов, метод, использованный в монографии [5], неприменим тоже. В то же время для решения сформулированной задачи достаточно методов вариационного исчисления, теории обобщенных функций и теоремы Фубини [8], поэтому будем поступать так.

Негладкий, континуально многозначный или разрывной интегрант можно представить с помощью функции включения H(x) (1.2) или ее производных, т.е. d -функции (1.5) и ее производных, используя их фильтрующие свойства. При варьировании функционала I все производные будем понимать в обобщенном смысле

.

Заметим, что этот интеграл теперь имеет математический и физический смыл, а не является "просто символом", как при классическом определении d -функции.

По общему правилу [9-12] введем однопараметрическое семейство кривых , где d h(t)-произвольная функция из Lp[a,b], a - малый параметр. Подставляя в операторы (2.1), а операторы (2.1) в функционал (2.2) и дифференцируя I по a , получим вариацию функционала d I и приравняем ее нулю:

Рекомендуем скачать другие рефераты по теме: менеджмент, сочинение бульба.



Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки