Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Проводя семантический анализ сюжетных задач, Л. М. Фридман [3] выделил следующие виды отношений, связывающих величины и их значения: отношение соединения; отношение отнимания; отношение сравнения (если величина задана двумя своими значениями): разностное отношение или кратное отношение двух значений величины, отношение разбиения (разделения); отношение-зависимость. Эти отношения являются уже не бинарными, а тернарными.

Будем рассматривать задачу как систему, т.е. как множество элементов, находящихся в определенном отношении друг к другу, причем это отношение обладает определенным свойством [4]. При построении моделей систем нужно учитывать то важное обстоятельство, что будучи аналогом системы модель не может достигнуть степени сложности оригинала. В модели стремятся отразить какое-нибудь одно отношение или структуру, специально выделенную для исследования. Поэтому моделирование по своей логической структуре напоминает умозаключение по аналогии. Вывод по аналогии о некоторых свойствах модели может быть экстраполирован на оригинал (систему) только в том случае, если отношения между элементами модели и системы установлены по одним и тем же свойствам и понимаются в одном и том же смысле. Эти отношения являются внутренними [4]. Отношение между величинами в задаче (отношение равенства) может быть установлено по разным свойствам:

a·b = c - по мультипликативным свойствам;

a+b = с - по аддитивным свойствам.

В дереве дуги задают бинарное отношение между вершинами. В задаче же отношение между величинами является тернарным, и устанавливается оно по разным свойствам. Поэтому будем рассматривать дерево, в котором фиксируется свойство, по которому установлено тернарное отношение равенства и называть его дерево-оператор (в дальнейшем просто дерево).

Моделирование сюжетных задач с помощью дерева рассмотрим на примере структурирования простейших задач. Структурирование - мыслительная деятельность по установлению отношений между величинами задачи. Для этого, используя восходящий анализ, построим граф - поиск решения задачи [5].

Задача I.1. Скорость велосипедиста 15 км/ч. Какое расстояние он проедет за 2 часа?

В задаче рассматривается одна ситуация - равномерное движение велосипедиста, характеризующееся тремя взаимосвязанными величинами: скорость движения V, время движения t и пройденный путь S. Эти величины связаны между собой формулой S = V·t. Если отвлечься от конкретного содержания задачи, то, обозначив первую величину через a, вторую - через b и третью - через c, получим зависимость между этими величинами: a·b = c.

Если рассматривать задачу как систему, то элементами ее решения будут значения величин (среди них два структурных элемента - известны, а одно значение - путь, является искомым); между величинами установлено тернарное отношение равенства по мультипликативному свойству. Ясно, что отношение является внутренним.

Итак, есть множество, состоящее из трех величин, между значениями этих величин установлено отношение равенства, следовательно, есть все формальные предпосылки для построения модели решения задачи в виде дерева (рис. 3):

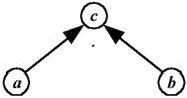
Рис. 3

c = a·b. В силу обратимости операций умножения и деления можно найти a = c/b или b = c/a.

Моделью решения сюжетной задачи является дерево. Оно характеризует структуру решения сюжетной задачи и сложность решения, отождествляемую со сложностью дерева:  = 2·3 = 6. Структурными элементами решения задачи являются вершины дерева.

Задача I.2. Из двух пунктов навстречу друг другу выехали два велосипедиста. Найти их скорость сближения, если скорость первого 15 км/ч, а скорость второго 13 км/ч.

В задаче задана одна величина a - скорость и три ее значения, из которых два известны, и одно искомое - скорость сближения. Дерево (рис. 4а) характеризует отношение сложения : a = a1+a2. В силу обратимости операций сложения и вычитания можно найти a1 = a-a2 или a2 = a-a1. Сложность решения задачи:  = 2·3 = 6.

Структурными элементами решения задачи являются три значения величины.

Поскольку в одной и той же задаче могут быть как отношение соединения, так и отношение отнимания, то для этих отношений целесообразно рассмотреть два дерева (рис. 4а и 4б).

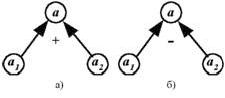
Рис. 4

Задача I.3. Скорость первого велосипедиста 12 км/ч, а скорость второго на 3 км/ч больше. Какова скорость второго велосипедиста?

Величина, рассматриваемая в задаче, - скорость задана двумя значениями: скорость первого велосипедиста a1 = 12 км/ч и скорость второго велосипедиста a2 - искомое значение. Имеющееся же в условии задачи данное: "на 3 км/ч больше" - не является значением рассматриваемой величины, а есть размер разностного сравнения заданных двух значений величины - скорости.

Дерево характеризует отношение разностного сравнения: a2 = a1+3 (рис. 5). Сложность решения задачи:  = 2·3 = 6. Структурными элементами решения задачи являются два значения одной величины и размер разностного сравнения.

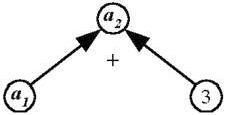
Рис. 5

Рекомендуем скачать другие рефераты по теме: банк курсовых, дипломы грамоты.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки