Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата



Вона носит назву формули Сімпсона (Th. Simpson); цією формулою користуються для наближенного обчислення інтегралів частіші, аніж формулами прямокутников і трапецій, бо она – при тих же затратах – дає зазвичай більш точний результат.

Залишковий член формули прямокутників.

Почнемо з формули (4). Припустимо, що у проміжку 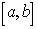функція 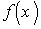має неперервні похідні перших двох порядків. Тогді, розкладая 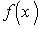(по формулі Тейлора) за степенями двочлена 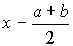аж до його квадрату, будемо мати для всіх значень 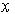в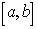

,

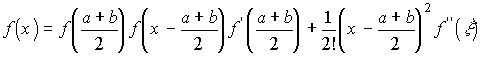де 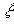міститься між 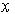та 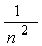і залежить від .

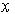Якщо проінтегрувати цю рівність у проміжку від 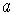до 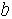, то другий член зправа зникне, бо

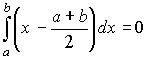(11)

Таким чином, отримаємо

,

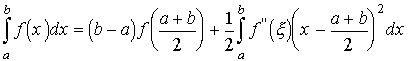так, що залишковий член формули (4), який поновлює її точність має вигляд

.

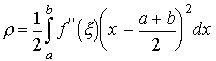Позначив через 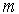і 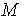, відповідно найменьше та найбільше значення неперервної функції 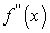у проміжку 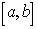і коростуючись тим, що другий множник підінтегрального виразу на змінює знака, за узагальненою теоремою про середне можемо написати

,

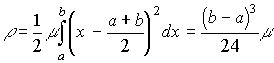де 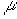міститься між точкам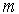и и 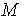. По відомій властивості неперервної функції, знайдеться в 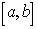така точка 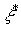, що 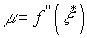, і остаточно

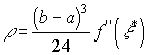. (12)

Якщо зараз розділити проміжок 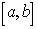на 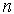рівних частин, то для кожного часткового проміжку 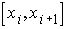будемо мати точную формулу

.

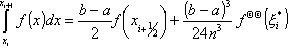
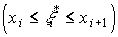Додавнши ці равенства (при 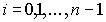) почленно отримаємо при звичайних скорочених позначеннях

,

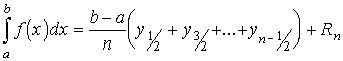де вираз

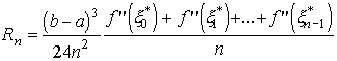
і є залишковий член формули прямокутників (1). Так як вираз

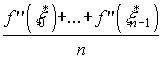
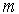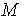також знаходиться між і , то і він представляє одне із значень функції .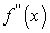

Рекомендуем скачать другие рефераты по теме: договора диплом, шпаргалки по математике транспорт реферат, конспекты бесплатно.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки