Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

Блок 4. Этот блок полностью соответствует соответствующему блоку в общем алгоритме субоптимизации на многообразиях для задачи выпуклого программирования.

 

3.8. Некоторые особенности вычислительной схемы метода субоптимизации на многообразиях для задачи квадратичного программирования.

В этой части будет рассмотрен вычислительный аспект процедуры субоптимизации и показаны некоторые ее замечательные свойства.

Выше было показано, что решение каждой вспомогательной задачи метода субоптимизации сводится к поиску разложения некоторого вектора R размерности (m+n) по базису UÁ 1,Á 2 ; при этом на соседних итерациях базисы отличаются лишь каким-то одним из векторов.

Как было показано выше, существуют четыре возможных альтернативы при переходе от одного базиса к другому, задающие четыре типа операций:

1. От UÁ 1 к UÁ 2 (Á 2=Á 1 j0 ) при помощи замены в базисе вектора Pm+n+j0 на Pm+j0 .

2. От UÁ 1 к UÁ 2,Á 1 (Á 2=Á 1 j0 U r) при помощи замены в базисе вектора Pm+r на Pm+j0 .

3. От UÁ 2,Á 1 (Á 2=Á 1 j0 U r) к UÁ 2 при помощи замены в базисе вектора Pm+n+j0 на Pm+n+r .

4. От UÁ 2,Á 1 (Á 2=Á 1 j0 U r) к UÁ 2',Á 2' (Á '2=Á 2 U r', Á '1=Á 1 U r' ) при помощи замены в базисе вектора Pm+r на Pm+n+r' .

Процедура разложения вектора R по базису эквивалентна решению системы линейных уравнений вида

где B - базисная часть матрицы P (то есть матрица, составленная из столбцов матрицы P , соответствующих векторам данного базиса). Решение уравнения есть процедура, эквивалентная обращению матрицы B.

Из общего вида матрицы P (3.2.4) можно получить общий вид матрицы B, которая также имеет блочную структуру следующего вида:

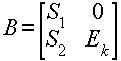
Рекомендуем скачать другие рефераты по теме: реферат предприятие, реферат по русскому.



Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки