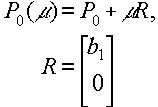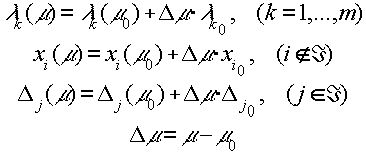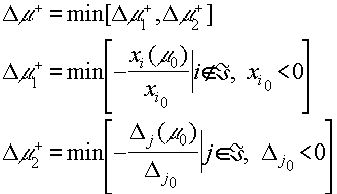Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

(4.1.3)

Разложив вектор R по указанному базису, и подставив это разложение в (4.1.3), получим следующие выражения для коэффициентов разложения (4.1.2):

(4.1.4)

Здесь - коэффициенты разложения вектора R по базису. Условием нарушения оптимальности решения является факт обращения в ноль одного из неотрицательных коэффициентов (4.1.4). Отсюда следует, что интервал, на котором исходное решение является оптимальным, является отрезком следующего вида:

(4.1.5)

где

(4.1.6)

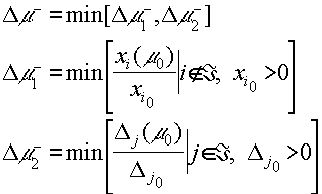
а

(4.1.7)

Из выражений (4.1.4) вытекает также тот факт, что на интервалах (4.1.5) вектор-функция x*(m ) представляет собой отрезок прямой в пространстве En , и является линейной. Стало быть, значения целевой функции на интервале представляют собой параболу.

 

4.3 Применение метода субоптимизации на многообразиях к решению параметрической задачи квадратичного программирования.

Непосредственно из вышеизложенного следует алгоритм решения задачи квадратичного программирования с параметром в правых частях ограничений:

1. В начальной точке интервала допустимых значений параметра строится решение задачи квадратичного программирования с помощью метода субоптимизации, описанного выше.

2. С помощью формул (4.1.6-4.1.7) определяется интервал на котором полученное решение остается оптимальным.

3. В правой точке полученного интервала строится решение задачи квадратичного программирования методом субоптимизации на многообразиях. Поскольку в этой точке существуют два оптимальных базиса, с целью предотвращения зацикливания в качестве начального базиса для решения задачи предлагается использовать предыдущий оптимальный базис (если решение потеряло оптимальность) или предыдущий оптимальный базис с исключенными векторами, чьи базисные переменные обратились в ноль.

 

 

5.Экономическая часть

Рассмотрим применение описанной теории к задаче определения оптимального портфеля ценных бумаг. Сформулируем задачу:

Имеется n видов ценных бумаг, имеющих доходности выражающиеся случайными величинами , распределенными по нормальному закону с параметрами . Помимо этого, имеется один вид ценных бумаг, дающий гарантированную доходность . Некий финансист ищет такой способ вложения единицы капитала в эти ценные бумаги, который обеспечил бы максимальный уровень дохода с заданной вероятностью a .

Покажем, что указанную задачу можно свести к задаче математического программирования:

Предположим, что вектор задает вложения финансиста в ценные бумаги соответствующего типа, а величина вложения в ценные бумаги с гарантированной доходностью. Тогда доход финансиста представляет собой случайную величину:

Очевидно, что характеристики этой случайной величины зависят от решения финансиста, и что эта величина распределена по нормальному закону:

Рекомендуем скачать другие рефераты по теме: реферат предприятие, реферат по русскому.



Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки