Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Таким образом, коммутативный (переместительный) закон умножения матриц, вообще говоря, не выполняется, т.е.  В частном случае коммутативным законом обладает произведение любой квадратной матрицы А  n-го порядка на единичную матрицу Е такого же порядка, т.е.

3. , .

Для этих матриц произведение как АВ ,так и ВА не существует.

, 

     

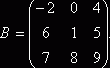
Получим , ВА – не существует.

Свойства умножения матриц.

Пусть А,В,С – матрицы соответствующих размеров (т.е. произведения матриц определены), l - действительное число. Тогда на основании определений операций и свойств действительных чисел имеют место следующие свойства:

(АВ)С = А(ВС) – ассоциативность.

(А+В)С = АС+ВС – дистрибутивность.

А(В+С) = АВ+АС – дистрибутивность.

l(АВ) = (lА)В = А(lВ).

ЕА = АЕ = А, для квадратных матриц единичная матрица Е играет роль единицы.

Приведем пример доказательства лишь одного свойства. Докажем, например, свойство 3.

Пусть для А=(аij), B=(bij), C=(cij) произведения матриц определены. Найдем элемент i-ой строки и j-го столбца матрицы А(В+С). Это будет число

аi1(b1j+c1j)+ аi2(b2j+c2j)+…+аin(bnj+cnj) =

(аi1b1j+ai2b2j+…+ainbnj)+ (аi1c1j+ai2c2j+…+aincnj).

Первая сумма в правой части равенства равна элементу из i-ой строки и j-го столбца матрицы АВ, а вторая сумма равна элементу из i-ой строки и j-го столбца матрицы АС. Рассуждение верно при любых i и  j, то свойство 3 доказано.

Упражнение 1. Проверьте свойство ассоциативности 1 для матриц:

, , .

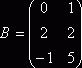Упражнение 2. Проверьте свойство дистрибутивности 2 для матриц:

, , .

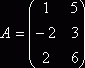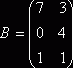Упражнение 3. Найти матрицу А3, если .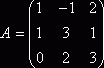

Вырожденные и невырожденные матрицы

Определение. Матрица называется вырожденной, если ее определитель равен нулю, и невырожденной, если определитель матрицы отличен от нуля.

Пример. ,  = 16-15 = 1  0; А – невырожденная матрица.

Рекомендуем скачать другие рефераты по теме: сочинение базаров, как оформить реферат.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки