Предыдущая страница реферата | 1  2  3  4  5

При i = j получим сумму произведений элементов i - ой строки на алгебраические дополнения этой же строки, такая сумма равняется значению определителя. Таким образом Сij = |А| = D - это элементы главной диагонали матрицы С. При i  j, т.е. для элементов Сij  вне главной диагонали матрицы С, имеем сумму произведений всех элементов некоторой строки на алгебраические дополнения другой строки, такая сумма равняется нулю. Итак,  = АА*

Аналогично доказывается, что произведение А на А* равно той же матрице С. Таким образом, имеем А*А = АА* = С. Отсюда следует, что

Поэтому, если в качестве обратной матрицы взять , то  Итак, обратная матрица существует и имеет вид:

.

Пример. Найдем матрицу, обратную к данной:

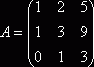
Находим D = |А| = -1 ¹ 0, А существует. Далее находим алгебраические дополнения элементов матрицы А:

А =  = 0 ; А =  = -1; А =  = 3;

А =  = -3; А =  = 3; А =  = -4;

А =  = 1; А =  = -1; А =  = 1;

А =

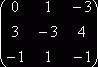
Скачали данный реферат: Bulygin, Sharov, Cedlic, Golovkin, Мосалев, Tolbanov.
Последние просмотренные рефераты на тему: контрольные 5 класс, реферат суды, культурология как наука, готовые рефераты.



Предыдущая страница реферата | 1  2  3  4  5

Поделитесь этой записью или добавьте в закладки