Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Напишем равносильную смешанную систему:

 

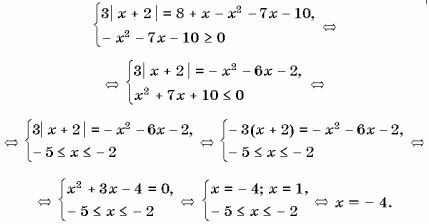
Ответ: х=-4

Пример 15 Решить графически уравнение |1 – x| - |2x + 3| + x + 4=0

Решение:

Представим уравнение в виде |1 – x| - |2x + 3| =-х – 4

Построим два графика у=|1 – x| - |2x + 3| и у=-х – 4

1) у=|1 – x| - |2x + 3|

Критические точки: х=1, х=-1.5

(1 – х) ________+________|______ +____________|_____-______ >

(2х +3) - -1.5 + 1 +

а) х< -1.5, (1– x)>0 и (2х + 3)<0, т.е функция примет вид у=1 – х + 2х + 3,

у=х + 4 –графиком является прямая, проходящая через две точки (0; 4), (-4; 0)

б)При -1.5 x <1, (1 – х)>0 и (2x +3) 0, т.е функция примет вид

у=1 – х – 2х -3, у=-3х – 2 –графиком является прямая, проходящая через две точки (0; -2), (-1; 1).

в)При х1, (1 – х)0 и (2х + 3)>0, т.е. функция примет вид у= -1 + х – 2х – 3,

у= -х – 4 –графиком является прямая, проходящая через две точки (0; -4),

(-4; 0).

График функции у= - х – 4 совпадает с графиком у=|1 – x| - |2x + 3|, при х1,

Поэтому решением являются все х1 и х= -4

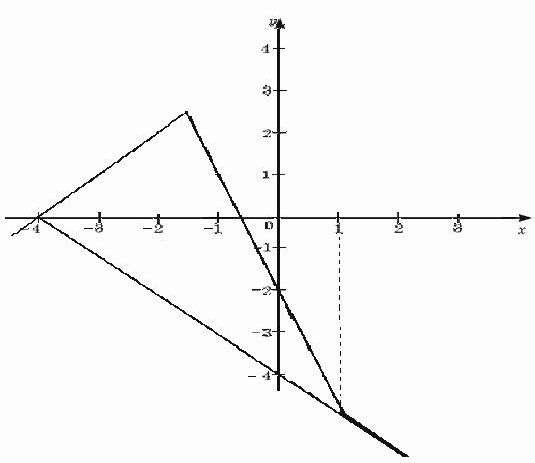
Ответ: х1,х= -4

Аналитическое решение.

y=|1 – x| - |2x + 3|

y=-x – 4

Рекомендуем скачать другие рефераты по теме: изложение русский язык 6 класс, личные сообщения.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки