Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Графическое решение

Преобразуем уравнение: : 1 + |x| = 0.5

|x| =0.5-1

|x|=-0.5

Графиком функции  являются лучи - биссектрисы 1-го и 2-го координатных углов. Графиком функции  является прямая, параллельная оси OX и проходящая через точку -0,5 на оси OY.

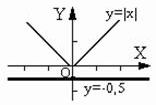
Рис. 11

Графики не пересекаются, значит уравнение не имеет решений (см. рис. 11).

Ответ: нет решений.

Пример 3. Решите аналитически и графически уравнение |-x + 2| = 2x + 1.

Решение:

Аналитическое решение

1-й способ

Прежде следует установить область допустимых значений переменной. Возникает естественный вопрос, почему в предыдущих примерах не было необходимости делать этого, а сейчас она возникла.

Дело в том, что в этом примере в левой части уравнения модуль некоторого выражения, а в правой части не число, а выражение с переменной, - именно это важное обстоятельство отличает данный пример от предыдущих.

Поскольку в левой части - модуль, а в правой части, выражение, содержащее переменную, необходимо потребовать, чтобы это выражение было неотрицательным, т. е.  Таким образом, область допустимых

значений модуля

Теперь можно рассуждать также, как и в примере 1, когда в правой части равенства находилось положительной число. Получим две смешанных системы:

(1) 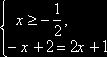 и (2)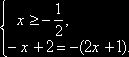

Решим каждую систему:

(1) 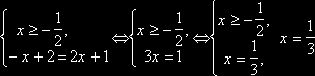 входит в промежуток  и является корнем уравнения.

(2) 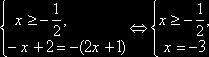 x = -3 не входит в промежуток  и не является корнем уравнения.

Ответ:

2-й способ

Установим, при каких значениях x модуль в левой части уравнения обращается в нуль:

Рекомендуем скачать другие рефераты по теме: изложение русский язык 6 класс, личные сообщения.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки