Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата



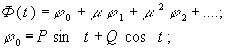(33)

P,Q-определяются формулами (31) (32).

§ 4 Исследование устойчивости периодических решений в области резонанса

Аналогично тому, как мы это делали в § 2, составим уравнение первого приближения, порожденное решением (33).

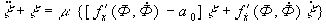
Решение опять будем искать в виде 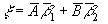. Однако нет необходимости проделывать все выкладки заново. Воспользуемся результатами § 2, приняв: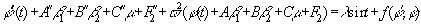

Из формул (22) 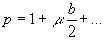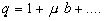(34) , тогда 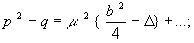D - тот же Якобиан, что и (32). Распишем его:

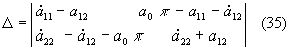
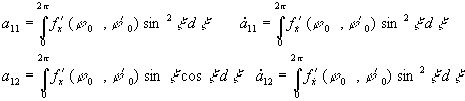(36)
;

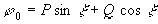Тогда, зная функцию f, мы можем вычислить D в виде функции P, Q и aо.

Заметим, что равенство (23 а) в нашем случае имеет вид:

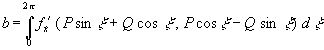; (37)

Опираясь на результаты исследования, полученных в § 2, нужно рассмотреть при исследовании устойчивости два случая: (при достаточно малых m )

1) p2 - q < 0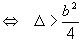

2) p2 - q > 0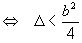

В первом случае устойчивость характеризуется условием q<1 или, что то же самое b<0.

Во втором случае 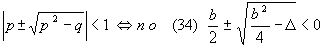(*) последнее может быть выполнено только, если b < 0, а D > 0. Нетрудно видеть, что необходимым достаточным условием в обоих случаях является b < 0, D > 0. (Это можно получить из неравенства (*) ).

§ 5 Применение общих формул, полученных в предыдущих параграфах, к теории захватывания в регенеративном приемнике для случая, когда характеристика - кубическая парабола.

Мы рассмотрим простой регенеративный приемник с колебательным контуром в цепи сетки, на который действует внешняя сила Ро sin w 1 t.

Дифференциальное уравнение колебаний данного контура следующее:

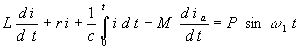(39)

Считая, что анодный ток зависит только от сеточного напряжения, а также, что характеристикой является кубическая парабола:

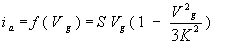(40)

S-крутизна характеристики, К - напряжение насыщения .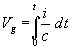

Далее, вводя обозначения: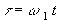

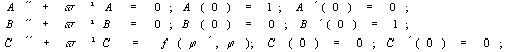
Получим дифференциальное уравнение для х:

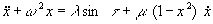(41)

А: (случай далекий от резонанса).

Для него применяем результаты § 1, полагая.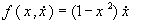

Исходное решение в не посредственной близости, к которому устанавливается искомое решение следующее:

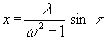
Если w > 1, т.е. w о > w 1, то разность фаз равна 0, если w < 1, то разность фаз равна p . В этом отношении все происходит в первом приближении также, как и при обычном линейном резонансе. Устойчивость определяется знаком b (b < 0).

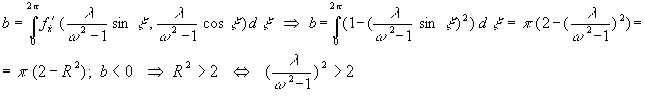(42).

Т.е. те решения, для которых выполняется это условие, устойчивы.

В: (область резонанса , § 3, 4).

В качестве исходного периодического решения, в непосредственной близости к которому устанавливается искомое, будет решение следующего вида: x = P sin t + Q cos t (P, Q - const).

Запишем уравнение, определяющее эти P и Q, т.е. соотношение (31) для нашего случая.

Рекомендуем скачать другие рефераты по теме: ответы 2011, шпоры по менеджменту.



Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки