Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

и обозначим

Интерполяционным кубическим сплайном, соответствующим данной функции и данным узлам, называеться функция , удовлетворяющая следующим усовиям:

а) на кождом сегменте функция является многочленом третьей степени;

б) функция , а так же ее первая и вторая производные непрерывны на ;

в)

Последнее условие называется условием интерполирования.

Докажем существование и единственность сплайна, определяемого перечисленными условиями (плюс некоторые граничные условия, которые будут введены в процессе доказательства). Приводимое ниже доказательство содержит также способ построения сплайна.

На каждом из отрезков будем искать функцию в виде многочлена третьей степени

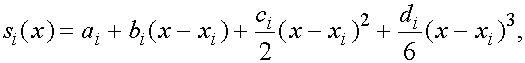(1)

где - коэффициенты, подлежащие определению. Выясним смысл введенных коэффициентов. Имеем

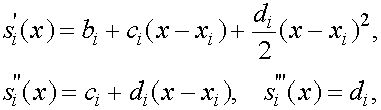
поэтому

Из условий интерполирования получаем, что

Доопределим , кроме того , .

Далее , требование непрерывности функции приводит к условиям

Отсюда,учитывая выражения для функций получаем при уравнения

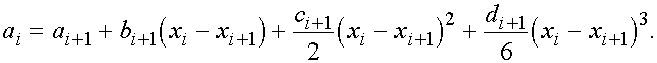Обозначая перепишем эти уравнения в виде

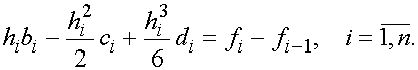(2)

Условия непрерывности первой производной

приводят к уравнениям

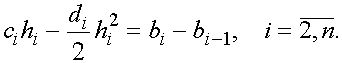(3)

Рекомендуем скачать другие рефераты по теме: ответы школа, свобода реферат.



Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки