Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Пусть m=2, т.е.

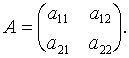
Если то утверждение теоремы выполняется при Р=Е, где Е - единичная матрица второго порядка. Если , то , т.к. При этом у матрицы

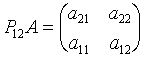
все угловые миноры отличны от нуля.

Пусть утверждение теоремы верно для любых квадратных матриц порядка m-1. Покажем, что оно верно и .для матриц порядка m. Разобьем матрицу А порядка m на блоки

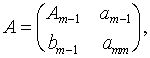
где

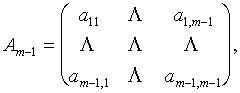
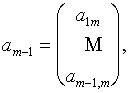
Достаточно рассмотреть два случая : и . В первом случае по предположению индукции существует матрица перестановок порядка m-1 такая, что имеет отличные от нуля угловые миноры. Тогда для матрицы перестановок

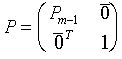
имеем

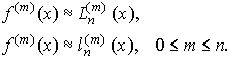
причем . Тем самым все угловые миноры матрицы РА отличны от нуля.

Рассмотрим второй случай, когда . Т.к. , найдется хотя бы один отличный от нуля минор порядка m-1 матрицы А, полученный вычеркиванием последнего столбца и какой-либо строки. Пусть, например,

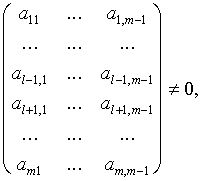
где .

Переставляя в матрице А строки с номерами l и m, получим матрицу , у которой угловой минор порядка m-1 имеет вид

и отличается от (23) только перестановкой строк. Следовательно, этот минор не равен нулю и мы приходим к рассмотренному выше случаю.

Теорема доказана.

ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ МЕТОДОМ ГАУССА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА.

Рекомендуем скачать другие рефераты по теме: ответы школа, свобода реферат.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки