Дифференциальные уравнения I и II порядка Введение.

Исследование поведения различных систем (технические, экономические, экологические и др.) часто приводит к анализу и решению уравнений, включающих как параметры системы, так и скорости их изменения, аналитическим выражением которых являются производные. Такие уравнения, содержащие производные, называются дифференциальными. Рассмотрим следующий пример из области рекламного дела.

При организации продажи нового товара торговым предприятиям зачастую приходится прибегать к услугам рекламы. Для того, чтобы последняя была успешной и современной, необходимо знать закон распространения информации о новом товаре среди ее потенциальных покупателей. Найдем вид указанной закономерности при следующих предположениях относительно рассматриваемого процесса.

Пусть N – общее число потенциальных покупателей нового товара, x(t) – число покупателей, знающих к моменту времени t о поступлении в продажу нового товара, [N-x(t)] – число покупателей еще не имеющих информации о товаре.

Предположим, что информация о товаре распространяется среди покупателей посредством их общения между собой. Будем считать, что в течение достаточно малого промежутка времени возможна встреча лишь двух покупателей, и вероятность этой встречи считаем равной P. Вероятность того, что при встрече покупатель, знающий о товаре, встретиться с покупателем, еще не имеющем информации о товаре, равна (N-x)/N. Тогда скорость изменения величины x(t) в момент t равняется px(N-x)/N систематическому ожиданию числа покупателей впервые узнавших о товаре. Таким образом, получаем уравнение

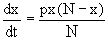или .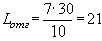

Данное уравнение содержит величину x и ее производную 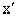, т.е. является дифференциальным. Решая полученное уравнение, найдем вид зависимости величины x от t:

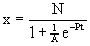, где параметр A подбирается, исходя из условия x=x0 в некоторый момент t=t0. Например, если при t=0 величина x(0)=g N (g - доля покупателей, обладающих информацией о товаре к началу рассматриваемого процесса), то 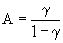. На рис. 1 показан график искомой функции x=x(t). В экономической литературе график известен как логистическая кривая.

Отметим, что логистическая кривая дает также представление о процессе распространения технологических новшеств, эпидемий и даже слухов.

В качестве второго примера рассмотрим задачу представления в виде уравнения однопараметрического семейства кривых, обладающих некоторым общим свойством.

Пусть однопараметрическое семейство кривых задается уравнением Ф(X,Y,C)=0, где C – параметр. Составим дифференциальное уравнение, которое описывает общее свойство присущее всем кривым данного семейства. Предположим, что отдельная кривая семейства заданных функций y=f(x,c). Тогда подставляя ее в общее уравнение семейства получаем тождество .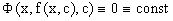

Предполагая дифференцируемость функции Ф(X,Y,C) и дифференцируя Ф(x,f(x,c),c) по x, получаем

.

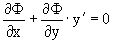Рассматривая последнее вместе с уравнением Ф(x,y,c)=0, т.е. рассматривая систему

,

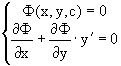и исключая в ней параметр C, в результате получим дифференциальной уравнение

,

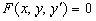описывающее свойство присущее всем кривым семейства.

Например, пусть семейство кривых представляет семейство гипербол xy=c.

Дифференцируя данное уравнение по x, получаем .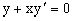

Так как при этом автоматически произошло исключение параметра c, то последнее уравнение, являясь дифференциальным, представляет семейство вышеуказанных гипербол.

1. Основные понятия и определения.

Определение. Уравнение, связывающее функцию y, ее аргумент x и ее производные, называется обыкновенным дифференциальным уравнением.

Обыкновенное дифференциальное уравнение символически можно записать в виде

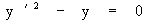или .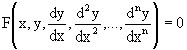

Определение. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.

Например:

Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.



1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки