Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата

из тождества

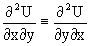
получаем, что для M(x,y) и N(x,y) должно выполняться условие

.

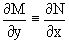Полученное условие является не только необходимым, но и достаточным для того, чтобы уравнение M(x,y)dx+N(x,y)dy=0

Было уравнением в полных дифференциалах.

Нахождение общего решения уравнения в полных дифференциалах проводится в два этапа.

На первом этапе функция U(x,y) рассматривается как функция только аргумента x, переменная y получает как бы фиксированное значение 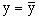. Тогда соотношению

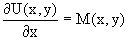
ставится в соответствие дифференциальное уравнение

.

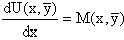Пусть его общее решение представляется в виде

.

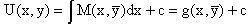Но так как решение уравнения зависит от y, то в общем решении постоянная c является функцией y, т.е. c=h(y). Следовательно, общее решение предыдущего дифференциального уравнения, снимая с y условие закрепления его значения, имеет вид

U(x,y)=g(x,y)+h(y).

На втором этапе находится вид функции h(y). Для этого обратимся к соотношению

,

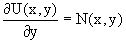в котором уже закрепляется как бы значение переменной x.

Используя данное соотношение и вид функции U(x,y), получаем дифференциальное уравнение, связывающее переменные h и y:

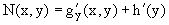или .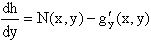

Интегрируя это уравнение, находим его общее решение

.

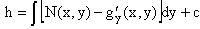Из 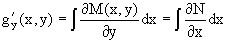, получаем окончательный вид функции U(x,y), а именно

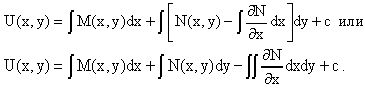
В последнем двойном интеграле вместо 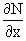можно взять функцию 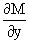(т.к. ). Тогда функция U(x,y) получает вид

Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.



Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки