
Экономико-математическое моделирование
Категория реферата: Рефераты по математике
Теги реферата: оформление титульного листа реферата, урок реферат
Добавил(а) на сайт: Конкордия.
Предыдущая страница реферата | 7 8 9 10 11 12 13 14 15 16 17 | Следующая страница реферата
можно заранее сформулировать поведение системы в будущем.
Марковские случайные процессы называют Марковскими цепями с вероятностью перехода в pij, когда процесс изучается в дискретные моменты времени.
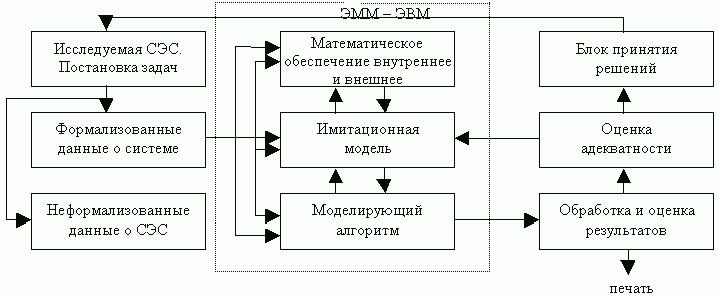
5.2. Имитационное моделирование систем и процессов.Применяется в случаях, когда нельзя заформализовать модель (описать аналитическим выражением) и в случае, когда система представляет собой многопараметрическую вероятностную экономическую систему. Кроме того, моделирование с помощью имитационных подходов применяется для систем больших размерностей и с большими внутренними связями.
Основные этапы моделирования:
анализ моделируемой систем, сбор необходимой информации, выделение проблемной области исследования и постановка задач на исследование; синтезирование (формирование, получение) необходимой математической модели области допустимых упрощений (ограничений), выбор критериев оценки эффективности и точности моделирования; разработка имитационной модели, алгоритма ее реализации, внутреннее и внешнее математическое обеспечение; оценка адекватности имитационной модели и контроль результатов экстремумов с последующей валидацией модели; анализ результатов моделирования с целью достижения заданной точности моделирования. 5.3. Имитационная модель и ее структура..При создании модели необходимо максимально использовать те параметры системы, которые поддаются формализации, то есть записи с помощью аналитических выражений.
 5.4. Метод Монте-Карло (метод статистических испытаний).
5.4. Метод Монте-Карло (метод статистических испытаний).
Данный метод родился в 1949 году благодаря усилиям американских ученых Дж. Неймана и Стива Улана в городе Монте-Карло (княжество Монако).
Метод Монте-Карло – численный метод решения математических задач при помощи моделирования случайных чисел.
Суть метода состоит в том, что посредствам специальной программы на ЭВМ вырабатывается последовательность псевдослучайных чисел с равномерным законом распределения от 0 до1. Затем данные числа с помощью специальных программ преобразуются в числа, распределенные по закону Эрланга, Пуассона, Релея и т.д.
Полученные таким образом случайные числа используются в качестве входных параметров экономических систем :
Q (x1, x2, x3,…,xn) Þ Qpt (min или max)
W : Bs (x1, x2, x3,…,xn) £ Rs
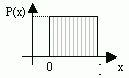
При многократном моделировании случайных чисел, которые мы используем в качестве входных параметров системы (модели), определяем математическое ожидание функции M(Q) и, при достижении средним значением функции Q уравнения не ниже заданного, прекращаем моделирование.
Статистические испытания (метод Монте-Карло) характеризуются основными параметрами:
D - заданная точность моделирования;
P – вероятность достижения заданной точности;
N – количество необходимых испытаний для получения заданной точности с заданной вероятностью.
Определим необходимое число реализаций N, тогда
(1 - D ) будет вероятность того, что при одном испытании результат не достигает заданной точности D ;
(1 - D ) N – вероятность того, что при N испытаниях мы не получим заданной точности D .
Тогда вероятность получения заданной точности при N испытаниях можно найти по формуле
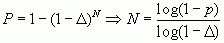 (19)
(19)
Формула (19) позволяет определить заданное число испытаний для достижения заданной точности D с заданной вероятностью Р.
|
D |
Значение Р |
|||
|
0,80 |
0,20 |
0,95 |
0,99 |
|
|
Предыдущая страница реферата | 7 8 9 10 11 12 13 14 15 16 17 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: | ||||