Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Упражнение 4: Постройте хотя бы еще одну развертку той самой призмы, две развертки которой изображены на рисунках.

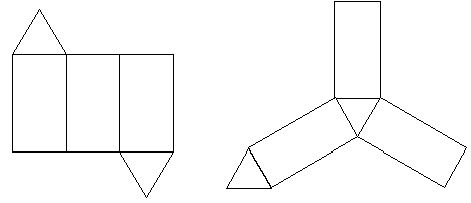
После этих упражнений понятие развертки и поверхности следует систематизировать.

Упражнение 5: Объясните связь рисунков (2) и (3) с призмой (1).

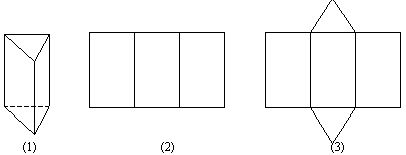
После этого упражнения ученики выявляют полную и боковую развертки.

Упражнение 6: Построить полные и боковые развертки следующих призм:

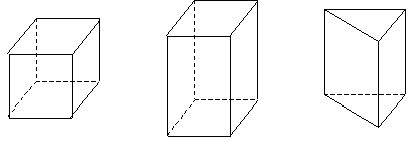IV этап: Введение понятия площади поверхности призмы

Цель: Углубление и расширение понятий площади поверхности на наглядно интуитивной основе.

Оборудование: модели призм.

Каждый ученик выбирает модель над которой будет выполнять следующие упражнения, которое позволит выяснить степень усвоения понятия развертки призмы.

Упражнение 1: Постройте развертку выбранной призмы. Выясните, есть ли равные многогранники в развертке, если есть то зарисуйте их.

Проблема 1: Как вычислить площадь поверхности развертки призмы?

Используя знания приобретенные ранее учащиеся убеждаются, что развертка призмы является объединением всех его граней, причем некоторые из граней равны друг другу.

Проблема 2: Как вычислить полную площадь поверхности призмы?

Соглашение 1: Площадью полной поверхности призмы называют сумму площадей всех граней призмы (Sп).

Соглашение 2: Площадью боковой поверхности призмы называется сумма площадей ее боковых граней (Sб)

Sп = Sб + 2 SоснSб = S1 + S2 + …

Упражнение 2: Поменяйте себе модель призмы, и вычислите боковую и полную ее поверхность.

Итог: Обобщим с помощью учащихся сведения о полной поверхности призмы и боковой поверхности призмы.

V этап: Введение понятия объема призмы

Цель: Углубить у учащихся интуитивно-наглядное понятие объема пространственных фигур.

Оборудование: модели призм.

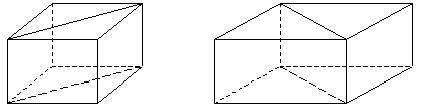
Разрежьте (пластилиновую модель призмы, плоскостью проходящей через диагональ основания. Какие получили фигуры?

В результате выполнения этого упражнения ученики получили две призмы с равными основаниями (основанием является прямоугольный треугольник), а все остальные соответствующие элементы призмы равны.

Упражнение 2: Как вычислить объем каждой из полученных призм?

Вывод: Каждая из полученных призм имеет объем равный половине объема данного параллелепипеда. (Объем параллелепипеда умеют вычислять в пятом классе).

Упражнение 3:

Дана призма, в основании которой треугольник. Как вычислить объем этой призмы?

Рекомендуем скачать другие рефераты по теме: диплом вуза, стратегия реферат.



Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки