
Геометрические свойства регулярного круглого конуса в пространстве
Категория реферата: Рефераты по математике
Теги реферата: курсовая работа по менеджменту, красный диплом
Добавил(а) на сайт: Бессонов.
Предыдущая страница реферата | 1 2 3 4 5 6 7 | Следующая страница реферата
где
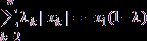 , 0 ≤
λ, λk ≤ 1};
, 0 ≤
λ, λk ≤ 1};
![]()
где
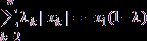 , 0 ≤
λ, λk ≤ 1}.
, 0 ≤
λ, λk ≤ 1}.
2.4. Общий случай. Для произвольного элемента х = (x1, ..., xn) и круглого регулярного конуса Kj (1) имеем:
![]()
где
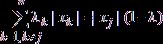 , 0 ≤
λ, λk ≤ 1};
, 0 ≤
λ, λk ≤ 1};
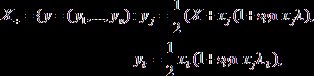
где
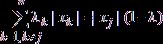 , 0 ≤
λ, λk ≤ 1};
, 0 ≤
λ, λk ≤ 1};
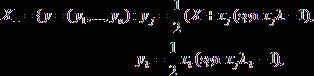
где
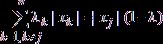 , 0 ≤
λ, λk ≤ 1};
, 0 ≤
λ, λk ≤ 1};
|
2 Труды молодых ученых, 2005 (1) |
3. Нахождение расстояния от элемента до конуса
Пусть элемент x принадлежит конусу К1, т.е. х1 ≥ X. В этом случае d(x, K1) = 0, а ближайшим элементом конуса является он сам.
Пусть элемент х принадлежит конусу – К1, т.е. -х1 ≥ X. В этом случае очевидно d(x, K1) = ||х||, а ближайшим элементом конуса является ноль.
Пусть х1 = 0 и элемент х не принадлежит конусу ±К1. Покажем, что d(x, K1) = ||х–||, а ближайшим элементом конуса является х+. Согласно следствию 2.2.13 [5], для этого необходимо найти функционал f Î К*1 такой, что ||f|| = 1, f(x+) = 0, f(x-) = ||x-||,
где x+ – x- = x, ||x+ + x-|| = ||x||.
В
качестве такого функционала выберем f=(1, –sgn x2, ...,–sgn xn). Для любого
элемента конуса аÎК1
справедливо f(а)=a1 –![]() , т. е. f положительный
функционал. Очевидно, что его норма равна единице. Элементы x+ и x–, вычисляемые по формулам 2.1, удовлетворяют условиям следствия 2.2.14 [5]. Кроме
того,
, т. е. f положительный
функционал. Очевидно, что его норма равна единице. Элементы x+ и x–, вычисляемые по формулам 2.1, удовлетворяют условиям следствия 2.2.14 [5]. Кроме
того,
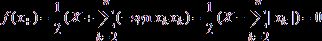 ,
,
![]() .
.
Учитывая, что ||x–|| = ![]() || (Х, x2, ...
, хn)|| = X, имеем, что f(x-) = =||x-||. Таким образом, условия следствия 2.2.14 [5]
выполняются полностью, и мы приходим к выводу, что
|| (Х, x2, ...
, хn)|| = X, имеем, что f(x-) = =||x-||. Таким образом, условия следствия 2.2.14 [5]
выполняются полностью, и мы приходим к выводу, что
d(x, K1) = || x-||
= ![]() =X, а x+
является ближайшим к х элементом конуса.
=X, а x+
является ближайшим к х элементом конуса.
3.4. Пусть X > х1 > 0. Положив λ = 0 в формулах 2.2, получим:
![]()
![]() ) .
) .
Рекомендуем скачать другие рефераты по теме: рефераты помощь, банк курсовых работ бесплатно.
Предыдущая страница реферата | 1 2 3 4 5 6 7 | Следующая страница реферата