Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Вычислим критические точки n1 и n2 функции f(n): Если a1b2 − a2b1 ≠ 0, то, учитывая

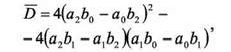
получим: Если D≥0,то

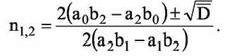
Если D < 0, то действительных критических точек нет. Если же a2b1 − a1b2 = 0, то

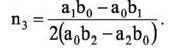
Нахождение угловых точек осуществляется в результате анализа функции

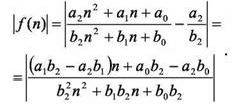
Угловые точки означают пересечение графика данной функции с осью абсцисс, то есть точки, где график функции резко меняет направление, поскольку данная функция является зеркальным отображением функции f ()n j (то есть отрицательные области графика зеркально отображаются относительно оси абсцисс).

Исходя из числителя функции, которая является линейной, очевидно нали-

чие либо одной такой точки, либо вовсе ее отсутствие.

Откуда

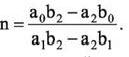
Итак, когда найдены B1 и B2 - точки разрыва, и E1, E2 - точки экстремума f()n и угловая точка G для функции

f ()n, определим интервал [nx;n0], на котором следует искать минимальный N()ε:

nx =max{B1,B2,E1,E2,G},

n0 - теоретически найденный номер аналитическим методом.

Теперь непосредственно рассмотрим вычислительные процедуры для нахождения N()ε, то есть три численных метода, которые применялись для вычисления минимального номера N(ε) при разработке программы "NUMBERS".

Метод золотого сечения

Золотое сечение, открытое Евклидом, состоит в разбиении интервала [а; b] точкой x на две части таким образом, чтобы отношение длины всего интервала к большей части было равно отношению большей части к меньшей:

Золотое сечение производят две точки:

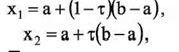
где

Рекомендуем скачать другие рефераты по теме: экзамены, антикризисное управление.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки