Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

(в качестве точки x будем

брать точку х1).

Алгоритм метода золотого сечения для интервала []nx;n0 J следующий:

1. Вычислить значение x.

2. Вычислить значение f()x.

3. Если f(x)< ε, то для дальнейшего деления оставляют интервал [nx;x].

4. Если f(x)≥ ε, то для дальнейшего деления оставляют интервал [x;n0].

Процесс деления продолжают до тех пор, пока длина интервала неопределенности не станет равной 1, то есть точки nx и n0 станут соседними. Искомым N(ε) будет номер n0.

При написании программы использованы стандартные функции: int - получение целой части числа, frac - получение дробной части числа.

Метод Фибоначчи

Как известно, числа Фибоначчи определяются соотношениями:

Используя числа Fn, строим n-точечный последовательный метод, который принято называть методом Фибоначчи. Как и метод золотого сечения, метод Фибоначчи состоит в задании на интервале [a;b] точки х1 или симметричной ей точки х2:

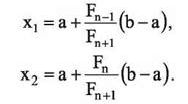
В качестве x - точки разбиения интервала будем брать точку хь Алгоритм метода Фибоначчи совпадает с алгоритмом метода золотого сечения. Единственный недостаток метода Фибоначчи в том, что нужно заранее задать количество проходов.

Интересно заметить, что

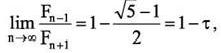
то есть при достаточно больших n (больше 10) точки разбиения методом Фибоначчи и золотого сечения практически совпадают. Это означает, что в данном случае метод Фибоначчи и метод золотого сечения по своей эффективности одинаковы, что и было подтверждено практическими испытаниями.

Метод дихотомии (бисекции)

Метод дихотомии состоит в разбиении интервала [a;b] точкой x пополам. Алгоритм метода дихотомии аналогичен алгоритму метода золотого сечения. Метод дихотомии является менее эффективным в данном случае, чем методы золотого сечения и Фибоначчи.

Описание лабораторной работы

Лабораторная работа по нахождению минимального номера N()ε может быть разделена на три этапа: I этап "Творческий поиск"

Студентам индивидуально-аналитическим методом оценок предлагается найти номер n0, начиная с которого выполняется xn − A < ε (например, ε = 0,05). Ввиду индивидуальности задания и различия способов оценки неравенства пути поиска решения проблемы могут быть весьма различными. IIэтап "Соревнование"

Данный этап подразумевает отыскание более точного значения номера n0 с аналогичными условиями выполнения. Студенты разделяются на m групп по 3 -4 человека, находят оптимальный общий метод оценки, благодаря чему вносится элемент соревнования, основанный на нахождении каждой из групп более точной оценки.

Преподаватель фиксирует найденные в группах номера nk (k = 1, 2, ….. , m) и оценивает правильность и эффективность оценочных процедур. /// этап "Нахождение минимального номера N()ε"

Данный этап является заключительным, поскольку именно здесь студенты получают возможность вычислить минимальный номер N(ε), начиная с которого выполняется неравенство

Предлагаются два возможных пути решения данной задачи: - Последовательное снижение по номерам вниз до тех пор, пока выполняется

Рекомендуем скачать другие рефераты по теме: экзамены, антикризисное управление.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки