
Исследование распределения температуры в тонком цилиндрическом стержне
Категория реферата: Рефераты по математике
Теги реферата: экзамен, защита диплома
Добавил(а) на сайт: Derevskov.
Предыдущая страница реферата | 4 5 6 7 8 9 10 11 12 13 14 | Следующая страница реферата
(5.1)
Введя новую переменную y = (U - , запишем (5.1) в виде:
(5.2)
0.18L/2 =0.0193. В качестве малого параметра возьмём .
Тогда, подставив y(x) в уравнение (5.2) и перегруппировав члены при одинаковых степенях , получим:
(5.3)
Ограничимся двумя первыми членами ряда:
Из (5.2) и (5.3) находим общее решение уравнения для y0:
где y0 с тильдой – частное решение данного неоднородного уравнения; y(1) и y(2) – линейно независимые решения однородного уравнения.
Корни уравнения:
y0общ = 1 + c1ch(px)+c2sh(px), где p = 0.01953
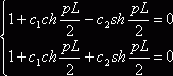 |
Константы найдём из граничных условий:
откуда с1 = 0, с2 = -0,57; т.е. имеем функцию:
y0 = 1 - 0.57 sh(px)
Общее решение:
Частное решение:
Дифференцируя и подставляя в уравнение, получим:
А1 = 0; А2 = -0,1083; В1 = 0; В2 = 17,1569;
Тогда общее решение для y1 имеет вид:
с3 = 0; с4 = 0,0462
Перейдя к старой переменной U, получим:
Итоговое уравнение:
Пользуясь этой формулой, составим таблицу значений функции U(x):
|
x Рекомендуем скачать другие рефераты по теме: реферат по труду, педагогические рефераты. Предыдущая страница реферата | 4 5 6 7 8 9 10 11 12 13 14 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |