Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

u ({p( i1), p( i2)..., p( iS)}) = u(S).

Содержательный смысл функции pu состоит в том, что если в игре с характеристической функцией u поменять местами игроков согласно перестановке p, то получим игру с характерис- тической функцией pu.

Аксиомы Шепли.

1о. Аксиома эффективности. Если S – любой носитель игры с характеристической функцией u, то

= u(S)

Иными словами, “справедливость требует”, что при разделении общего выигрыша носителя игры ничего не выделять на долю посторонних, не принадлежащих этому носителю, равно как и ничего не взимать с них.

2о. Аксиома симметрии. Для любой перестановки p и iÎN должно выполняться

(pu) = ji (u),

т.е. игроки, одинаково входящие в игру, должны “по справедливости” получать одинаковые выигрыши.

3о. Аксиома агрегации. Если есть две игры с характеристическими функциями u¢ и u¢¢, то

j i (u¢ + u¢¢) = j i (u¢) + j i (u¢¢),

т.е. ради “справедливости” необходимо считать, что при участии игроков в двух играх их выигрыши в отдельных играх должны складываться.

Определение. Вектором цен (вектором Шепли) игры с характеристической функцией u называется n-мерный вектор

j (u) = (j1(u), j2(u), ..., jn(u)),

удовлетворяющий аксиомам Шепли.

Существование вектора Шепли вытекает из следующей теоремы

Теорема. Существует единственная функция j, определённая для всех игр и удовлетворяющая аксиомам Шепли.

Определение. Характеристическая функция wS(T), определённая для любой коалиции S, называется простейшей, если

wS(T) =

Содержательно простейшая характеристическая функция описывает такое положение дел, при котором множество игроков S выигрывает единицу тогда и только тогда, когда оно содержит некоторую основную минимальную выигрывающую коалицию S.

Можно доказать, что компоненты вектора Шепли в явном виде запишутся следующим образом

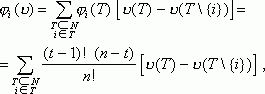
где t – число элементов в T.

Вектор Шепли содержательно можно интерпретировать следующим образом: предельная величина, которую вносит i-й игрок в коалицию T, выражается как

u(T) - u(T {i})

Рекомендуем скачать другие рефераты по теме: конспект урока 10 класс, англия реферат.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки