Математическое ожидание и дисперсия для интервальных и пропорциональных шкал. Доверительные интервалы.

С.В. Усатиков, кандидат физ-мат наук, доцент; С.П. Грушевский, кандидат физ-мат наук, доцент; М.М. Кириченко, кандидат социологических наук

Рассмотрим случай, когда в проводимом эксперименте числовая шкала имеет единицу измерения, т.е. про полученные числовые величины всегда можно сказать, насколько одно больше другого. Например, х - это число ошибок, допущенных при каком-либо тестировании, или число правильных ответов. Обозначим х1,...,хк деления этой шкалы, а n1,...,nk - частоты или число попаданий случайной величины х на каждое из этих делений. Например, в тестировании: шкала х1=0 правильных ответов, ..., хк=к-1 правильных ответов; n1 тестируемых не дали ни одного правильного ответа..., nk тестируемых дали к-1 правильных ответов.

Математическим ожиданием или просто средним называется число mx, вычисляемое по следующему правилу:

mx= (n1x1+.....+nkxk),

где n=n1+...+nk - общее число испытаний

Дисперсией называется число , вычисляемое по следующему правилу:

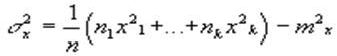чаще используется число , которое называется стандартным отклонением.

Например, группу из n=11 учащихся опросили и получили следующее число правильных ответов:

Главная | Партнеры | Лучшие рефераты

Обратная связь

Рефераты | Рефераты по математике | Математическое ожидание и дисперсия для интервальных и пропорциональных шкал. Доверительные интервалы | страница реферата 1 | Большая Энциклопедия Рефератов от А до Я    Все рефераты, курсовые, дипломы, шпаргалки, сочинения, изложения, решебники, конспекты являются общедоступными    Копирование и размещение в интернете разрешается только при наличии активной индексируемой ссылки на Ahaha.ru

© 2006-2020 «Ahaha.ru»