Механические колебания в дифференциальных уравнениях

Реферат Выполнил: студент гр. МХТ-02 Казаков Василий Васильевич

Магнитогорский государственный технический университет им. Г.И. Носова

Магнитогорск 2003

Колебаниями  называются процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качания маятника часов, переменный электрический ток и т.д. При колебательном движении маятника изменяется координата центра масс, в случае переменного тока колеблются напряжение и сила тока. Физическая природа колебаний может быть разной, однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Рассмотрим механические колебания.

Гармонические колебания.

Гармоническими колебаниями называются колебания, при которых изменяющаяся величина изменяется по закону синуса (косинуса).

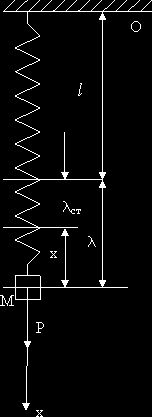
Пусть груз весом Р подвешен на вертикальной пружине, длина которой в естественном состоянии равна . Груз слегка оттянут книзу и затем отпущен. Найдем закон движения груза, пренебрегая массой пружины и сопротивлением воздуха.

Решение

Направим ось Ох вниз по вертикальной прямой, проходящей через точку подвеса груза. Начало координат О выберем в положении равновесии груз, то есть в точке, в которой вес груза уравновешивается силой натяжения пружины.

Пусть l означает удлинение пружины  в данный момент, а lст—статическое удлинение, т.е. расстояние от конца нерастянутой пружины до положения равновесия. Тогда l=lст+х, или l-lст=х.

Дифференциальное уравнение получим из второго закона Ньютона: F=ma,   где m=P/g—масса груза а—ускорение движения и F—равнодей-ствующая приложенных к грузу сил. В данном случае равнодействующая слагается из силы натяжения пружины и силы тяжести.

По закону Гука сила натяжения пружины  пропорциональна её удлинению: Fупр=-сl, где с – постоянный коэффициент пропорциональности называемый жесткостью пружины.

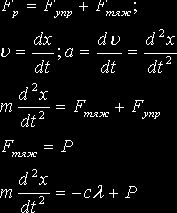
Так как в положении равновесия сила равновесия сила натяжения пружины уравновешивается весом тела, то P= сlст. Подставим в дифференциальное уравнение выражение Р и заменим  l-lст через х, получится уравнение в виде:

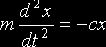
или, обозначив с/m через k2,

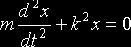                                                  (1)

Полученное уравнение определяет так называемые свободные колебания груза. Оно называется уравнением гармонического осциллятора. Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение:

имеет мнимые корни , соответственно этому общее решение

Для выяснения физического смысла решения удобнее привести его к другой форме, введя новые произвольные постоянные. Умножив и разделив на , получим:

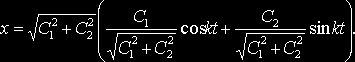
Если положить

  

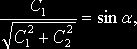
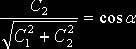
то

Рекомендуем скачать другие рефераты по теме: сочинение, реферат расчеты.



1  2  3  4  5  6  7  8 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки